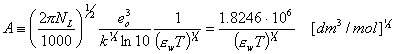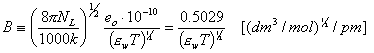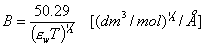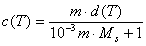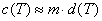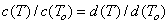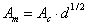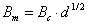© A.W.Marczewski 2002
Reload Data&Tools
Activity coefficients of ions in aqueous solutions:
Data sources
- Formulas
- Debye-Hückel formula
Activity, molar concentration, molality and ionic strength,
A and B - parameters of Debye-Hückel formula (for molar concentration and molality)
Molar concentration and molality - temperature dependences
- Figures
- Dependences of Debye-Hückel constants A and B on temperature
- Dependence of dielectric constant on temperature
Activity coefficients of ions in solutions may be calculated by Debye-Hückel formula (here average coeffcient for Mez+ : Xz- electrolyte, for individual ions use single z value):
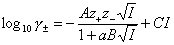
where:
γ is activity coefficient given as the ratio of activity and concentration (or analogously for molality, m):
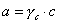
and average coefficient for Mev+Xv- electrolyte may be calculated from individual ionic coefficients by:
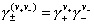
A, B, C are constants (see below), a is ionic size (of the hydrated ion!) and I is ionic strength (identical with concentration - or molality - for 1:1 electrolytes):
![Ionic strength for molar concentrations [mol/dm3]](activity/xIonSc-fx.gif.pagespeed.ic._QSjG6qGIF.png) or
or
![Ionic strength for molality [mol/kg]](activity/xIonSm-fx.gif.pagespeed.ic.Po6c5M5SaR.png)
C is determined experimentally, however A and B may be calculated from Debye-Hückel theory (below formulas for ionic strength defined as molar concentration, for B the formulas depend also on the units of ion size, e.g. for Na+ a = 450pm or 4.5A):
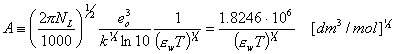
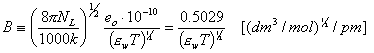
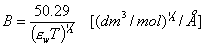
Why do we often use molality m (ratio of solute quantity [mol] to the amount of solvent [kg]) instead of molar concentration (solute quantity to solution volume)? Molality is temperature independent value, whereas molar concentration changes with temperature along solution density changes:

If we express concentration through molality, a dependence on solution temperature appears, too:
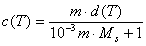
This formula may be simplified for dilute solutions:
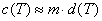
(For commonly used water solution temperatures and units ( 1 g/cm3 = 1 kg/dm3 ), molar concentration and molality is expressed by the same numbers.)
Then, concentrations are temperature dependent exactly like solution density:
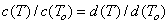
Then it is easy to show, that the above A, B constants defined for molar concentrations may be recalculated for use with ionic strength, I, expressed as molality, m [mol/kg]:
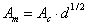 and
and
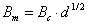
where index "c" denotes values calculated for I [mol/dm3] and d is solution density d [g/cm3] or d [kg/dm3].
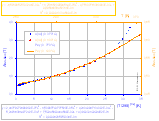
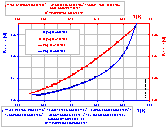
Both A and B depend on temperature and dielectric constant of solution (for dilute solutions, the dielectric constant is the same as dielectric constant of water - see below).
A(T), A(T9/2) (better polynomial fit in 0..370°C range) and B(T) graphs with polynomial fits:
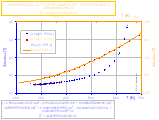
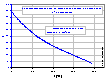
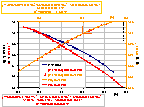
The dielectric constant of water depends on temperature (see left fig.). Various powers of the product (εT) are also presented as functions of temperature (see also tables of water properties):
Top
Main page
E-mail addresses are modified to in order to prevent spamming / mail-abuse:
in e-mail remove spaces, replace " AT@AT " by "@"
Send a message to Adam.Marczewski AT@AT umcs.lublin.pl
Disclaimer
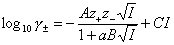
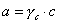
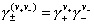
![Ionic strength for molar concentrations [mol/dm3]](activity/xIonSc-fx.gif.pagespeed.ic._QSjG6qGIF.png) or
or
![Ionic strength for molality [mol/kg]](activity/xIonSm-fx.gif.pagespeed.ic.Po6c5M5SaR.png)