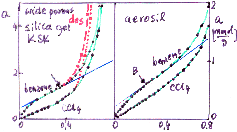
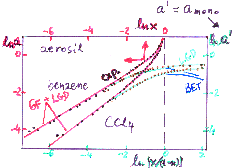
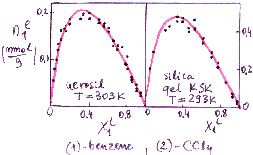
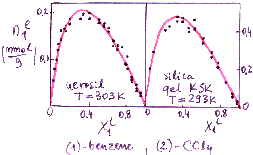
 Prediction of multicomponent adsorption for components with non-linearly correlated adsorption energy distributions.
(Here are model pictures and examples)
Prediction of multicomponent adsorption for components with non-linearly correlated adsorption energy distributions.
(Here are model pictures and examples)
Necessary theoretical background is given in:
multi-component GIEA and Energy correlation
Applicability - method requirements:
Proposed method assumes that a certain correlation (generally non-linear) exists between adsorption energies of various adsorbates on a solid surface. This energy correlation assumes that at least the order of site energies is the same for all components, i.e. if the site energy (it means of course adsorption energy of component on a site) order for a component "i" is:
EiA ≤ EiD ≤ EiC ≤ EiB
then for any other component "j" we must have at least:
EjA ≤ EjD ≤ EjC ≤ EjB
where A - D denote site types (a stronger condition where "≤" is replaced by "<" is easier to analyse).
Generally no limit of no. of components/active site exists. Energy distribution function may be discrete (like in the example above) or continuous. Prediction requires data for simple (single-component or binary) systems or at least some estimated values of heterogeneity parameters or energy dispersion σE values. However, this method will succeed only if its main assumption about sequence of adsorption energy magnitudes (or sequence of adsorption energy differences, e.g. Ein like Ejn and Ekn) being common for all single or binary systems is true. In solutions it is always reasonable to choose a "reference adsorbate" ("n") which should be as different from all other adsorbates as possible (e.g. organic solutes "1","2","3" vs. water reference, "n").
If adsorbates showing very specific interactions with the surface are used, the prediction may not be satisfactory if those interactions are different for those adsorbates (e.g. acid R-COOH and amine R-NH2 adsorbed on the surface having acidic and basic functional groups. In such a case the parts of adsorption energy distributions related to acid-base interaction cannot be predicted properly (This does not include adsorbate-adsorbate interaction, that should be taken into account by other methods: formation of ion pairs, association etc.). However, the non-specific part of adsorption energy - if it is large comparing to the specific one - may still lead to reasonable prediction of at least some of the parameters.
References
For more info consult these papers:
- "Unified Theoretical Description of Physical Adsorption from Gaseous and Liquid Phases on Heterogeneous Solid Surfaces and Its Application for Predicting Multicomponent Adsorption Equilibria", A.W.Marczewski, A.Derylo-Marczewska and M.Jaroniec, Chemica Scripta, 28, 173-184 (1988).
- "Correlations of Heterogeneity Parameters for Single-Solute and Multi-Solute Adsorption from Dilute Solutions", A.W.Marczewski, A.Derylo-Marczewska and M.Jaroniec, J.Chem.Soc.Faraday Trans.I, 84, 2951-2957 (1988), (doi).
- "A Simplified Integral Equation for Adsorption of Gas Mixtures on Heterogeneous Surfaces", A.W.Marczewski, A.Derylo-Marczewska and M.Jaroniec, Mh.Chem., 120, 225-230 (1989), (doi).
- "Prediction of the Heterogeneity Parameters for Adsorption of Multicomponent Liquid Mixtures on Solids", A.W.Marczewski, A.Derylo-Marczewska, M.Jaroniec and J.Oscik, Z.phys.Chem., 270(4), 834-838 (1989) (pdf, hi-res pdf available upon e-mail request).
- "Analysis of Experimental Data for Adsorption of Organic Substances from Dilute Aqueous Solutions on Activated Carbon", A.Derylo-Marczewska and A.W.Marczewski, Polish J. Chem., 71, 618-629 (1997)
- "A General Model for Adsorption of Organic Solutes from Dilute Aqueous Solutions on Heterogeneous Solids: Application for Prediction of Multisolute Adsorption", A.Derylo-Marczewska and A.W.Marczewski, Langmuir, 13, 1245-1250 (1997), (doi).
Prediction cases:
This method, described in details and tested on experimental data, may reasonably predict adsorption (or at least is able to estimate the magnitude of heterogeneity effects) in many situations:
- Prediction of adsorption in gas mixtures (required: single gas adsorption data for all components; useful: binary gas mixture data - if e.g. prediction of tertiary-mixture adsorption is wanted; quality of prediction - very good).
- Prediction of adsorption in multi-component dilute solutions (required: single solute adsorption data for all components; useful: binary dilute solute adsorption data - if e.g. prediction of tertiary mixture adsorption is wanted; quality of prediction - good or very good).
- Prediction of adsorption in liquid mixtures (required: single gas/vapour adsorption data for all components; useful: binary gas mixture data - if e.g. prediction of tertiary-mixture adsorption is wanted; quality: heterogeneity parameters are nicely estimated, other parameters may require correction) (for the prediction in e.g. tertiary systems, it is much better if binary liquid mixtures are available)
Necessary prediction steps:
- Prediction of adsorption in gas mixtures:
Measure single-component isotherms - calculate isotherm parameters - get energy distributions χi(Ei) - convert to Ei(F) and zi(F). Use General Integral Equation for mixtures, calculate isotherm data (if possible measure several isotherm points for mixed isotherm and correct parameters - mainly equilibrium constants). Another possibility is fitting all data together (see LSQ for multiple data sets) - it may require more points measured for mixture and/or additional weighting, however, it may result in a solution allowing for a wider range of prediction (though fitting quality for individual isotherms may be worse). We (me and my wife) used this method for fitting several hundreds of isotherm data points of solute and multi-solute adsorption on activated carbons (see below). - Prediction of adsorption in multi-component dilute solutions:
see prediction steps for gas mixtures (above) - Prediction of adsorption in liquid mixtures:
- From single vapor isotherm data - calculate energy distributions χi(Ei) - convert to Ei(F) and zi(F). Use General Integral Equation for mixtures:
- Calculate energy distributions of energy differences for suitable component pairs:
zin(F) = zi(F)-zn(F)
(determine "reference component" by choosing one with the smallest or one with the highest heterogeneity effects), then use calculate isotherm data by using suitable "competitive" form of 1-dimensional multi-GIEA i.e. the one for (n-1) component "in" pairs (if possible measure several isotherm points for mixed isotherm and correct parameters - mainly equilibrium constants). - Use original energy distributions zi(F) in a suitable form of multi-GIEA (for n individual components)
- Calculate energy distributions of energy differences for suitable component pairs:
- From binary liquid adsorption data - calculate energy distributions χij(Eij) - convert to Eij(F) and zij(F). Then use General Integral Equation for mixtures (its competitive form - for component pairs). All parameters of competitive adsorption (binary mixtures) should be given with respect to the same "reference component", i.e. (n-1) "ij" component pairs
- From single vapor isotherm data - calculate energy distributions χi(Ei) - convert to Ei(F) and zi(F). Use General Integral Equation for mixtures:
For 2 components and LF isotherm, LF isotherm is fitted -> common monolayer capacity, am, heterogeneity parameters mLF,1, mLF,2 and equilibrium constants K1 and K2 are obtained.
Energy functions ELF,1(F), ELF,2(F) and zLF,1(F) and zLF,2(F) are calculated from theoretical energy distributions χLF,i(E), then used in multi-GIEA.
By comparing predicted adsorption values with experimental ones one can slightly correct predicted theoretical isotherm(s) (e.g. by correcting individual Ki or competitive Kij equilibrium constants - energy distributions/energy dispersions/heterogeneity parameters should be OK).