© A.W.Marczewski 2002
A Practical Guide to Isotherms of ADSORPTION on Heterogeneous Surfaces
Reload Adsorption Guide
ADSORPTION: dispersion of adsorption energy
General Integral Equation /
GL (Generalized Langmuir) /
All equations (preview)
Energy Dispersion (General / Isotherm parameters / Calculation / Formulas )
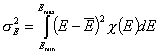 Data analysis - dispersion of adsorption energy σE:
Data analysis - dispersion of adsorption energy σE:
-
Calculation of adsorption energy dispersion σE allows to compare heterogeneities of various adsorption systems. This single value does not contain any information on energy distribution symmetry/asymmetry (in this aspect similar to global heterogeneity H), however if adsorption systems are similar and we may expect similar character of their energy distribution functions we may predict (or at least estimate) the behaviour of a mixed system. A short list of energy dispersion formulas is below.
- "Unified Theoretical Description of Physical Adsorption from Gaseous and Liquid Phases on Heterogeneous Solid Surfaces and Its Application for Predicting Multicomponent Adsorption Equilibria", A.W.Marczewski, A.Derylo-Marczewska and M.Jaroniec, Chemica Scripta, 28, 173-184 (1988) (pdf, hi-res pdf available upon e-mail request).
Relationships between parameters of various isotherms
Quite often, some adsorption data may be well described by more than one isotherm equation. If underlying energy distributions are of similar character (e.g. both are symmetrical quasi-gaussian), we may try to estimate parameters of another eqn. by using already determined parameters. In fact even if the energy distribution functions in question differ in symmetry etc. but available adsorption data cover only a section of coverage range (it also corresponds to a section of energy distribution) parameters assessed in such a way may still be useful. All depends on: "how large this isotherm/energy distribution section is", "how much both distributions differ one from another" (here one must say that the isotherms are not-so-much sensitive to the details of energy distributions!).
So in fact, what is important is not the details of energy distribution functions, but the course of isotherms - if they are "similar enough", everything should work well. In order to compare parameters of different but "similar enough" isotherms, one may use e.g. energy dispersion formulas listed below.
Here are papers that exploit this possibility:
- "Relationships Defining Dependence Between Adsorption Parameters of Dubinin-Astakhov and Generalized Langmuir Equations", M.Jaroniec and A.W.Marczewski, J.Colloid Interface Sci., 101, 280-281 (1984),
(doi).
- "Correlations Among the Parameters of Dubinin-Radushkevich and Langmuir-Freundlich Isotherms for Adsorption from Binary Liquid Mixtures", A.Derylo-Marczewska, M.Jaroniec, J.Oscik and A.W.Marczewski, J.Colloid Interface Sci., 117, 339-346 (1987),
(doi).
-
Calculation of energy dispersion - definitions
For some isotherm equations the energy dispersion σE may be calculated very easily (see there) by using one of the formulas below:
-
Classic definitions using differential distribution χ(E) of reduced adsorption energy, E = ε/RT:
- Average adsorption energy Eav and energy dispersion σE
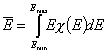
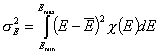
-
Definitions using integral form F(E) (and respectively its inverse form E(F)) of reduced energy distribution function χ(E):
- differential distribution function χ(E) and integral distribution function F(E):
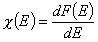
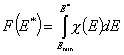
- Average adsorption energy Eav and energy dispersion σE
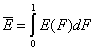
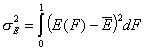
-
Definitions using integral form F(z) (and respectively its inverse form z(F)) of relative reduced energy distribution function χ(z), where relative reduced energy is defined as a difference of energy and average energy of a given distribution, z = E - Eav (then z(F) = E(F)-Eav ) :
- Relative reduced energy: z(F) = E(F)-Eav
- Differential distribution function χ(z) and integral distribution function F(z):
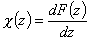
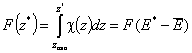
- Average relative adsorption energy ( zav = 0 ) and energy dispersion σE:
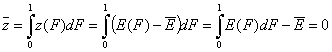
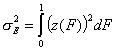
-
Energy dispersions for some isotherms:
- G - Gauss distribution is defined 2 parameters which are the same as average adsorption energy Eav = Eo and energy dispersion σE
- R - Rudzinski isotherm:
Eav = Eo (symmetrical distribution)
σE = π / (31/2 m)
- Sq - "Square"/UNILAN (continuous distribution) isotherm:
Eav = Eo = (Emin + Emax)/2 (symmetrical distribution)
σE = ΔE / (31/2 2)
- k - discrete distribution with k equally energy-spaced sites isotherm:
Eav = (Emin + Emax)/2 (symmetrical distribution)
σE = ΔE [(k+1)/(k-1)]1/2 / (31/2 2) , where k ≥ 2
- F - cut Freundlich continuous distribution ( χ(E) = m exp[-m(E-Emin) - 1] , E ≥ Emin ) isotherm:
Eav = Emin + 1/m
σE = 1/m
- LF - Langmuir-Freundlich isotherm (GL, m=n):
Eav = Eo (symmetrical distribution)
σE = (π/ 31/2) [(1 - m2)1/2 / m]
- GF - Generalized-Freundlich isotherm (GL, n=1):
Eav > Emin (asymmetrical distribution)
σE ≈ [(1 - m2)1/2 / m]
- T - Tóth isotherm (GL, m=1):
Eav < Eo (asymmetrical distribution, Eo char. energy)
σE ≈ 1.3 [(1 - n2)1/2 / n]
Energy Dispersion (General / Isotherm parameters / Calculation / Formulas )
General Integral Equation /
GL (Generalized Langmuir) /
All equations (preview)
Top
My papers
Search for papers
Main page
E-mail addresses are modified to in order to prevent spamming / mail-abuse:
in e-mail remove spaces, replace " AT@AT " by "@"
Send a message to Adam.Marczewski AT@AT umcs.lublin.pl
Disclaimer
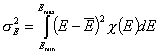 Data analysis - dispersion of adsorption energy σE:
Data analysis - dispersion of adsorption energy σE:
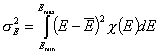 Data analysis - dispersion of adsorption energy σE:
Data analysis - dispersion of adsorption energy σE: