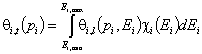 General Integral Equation of Adsorption (GIEA):
General Integral Equation of Adsorption (GIEA):Multicomponent systems
© A.W.Marczewski 2002
A Practical Guide to Isotherms of ADSORPTION on Heterogeneous Surfaces
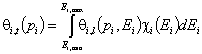 General Integral Equation of Adsorption (GIEA):
General Integral Equation of Adsorption (GIEA):
Multicomponent systems
General Integral Equation of Adsorption (GIEA) is a general formulation of adsorption isotherm involving energetical heterogeneity of the adsorption system (i.e. adsorbate-surface). The first attempt to do that was by Langmuir (1918) but it was represented by a summation not an integral.
Another similar in character Integral Equation of Adsorption is the Stoeckli integral equation for adsorption on microporous non-uniform solids.
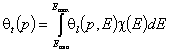 - for single gas adsorption
- for single gas adsorption
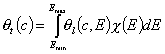 - for dilute single-solute adsorption
- for dilute single-solute adsorption
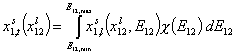 - for binary liquid adsorption
- for binary liquid adsorption
If you need just single gas/vapor, single solute (in dilute solution) or binary mixture adsorption start rather from General Integral Equation of Adsorption for single gas, single solute, binary liquid mixture.
Current page contains a reformulation of these simple cases consisting mostly of adding component indices required in n-component mixtures. However, this reformulation is heavily mixed with multicomponent formulas.
Simple cases reformulated
First, lets reformulate the simple cases (single gas, single solute, binary liquid mixture) in the way allowing to use component numbering necessary in multicomponent systems. It will also allow to use such defined parameters and functions in multicomponent systems consisting of components for which we have single-component (or binary) data.
Global (overall) isotherm of adsorption θt
Global (overall) isotherm of adsorption θt (i.e. relative surface coverage = (adsorbed amount) / (maximum amount adsorbed in monolayer)) is obtained by averaging of local coverage θl (adsorption energy dependent isotherm equation) corresponding to adsorption on energetically homogeneous surface. This averaging depends on the site's relative frequency or probability.
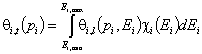 - for adsorption of single gas "i"
- for adsorption of single gas "i"
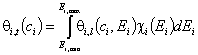 - for adsorption of dilute single-solute "i"
- for adsorption of dilute single-solute "i"
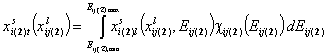 - for adsorption in binary liquid "i+j"
- for adsorption in binary liquid "i+j"
Multicomponent General Integral Equation of Adsorption
This formulation utilizes n-dimensional χ(n) or (n-1)-dimensional χ(*n) differential energy distribution function. The local adsorption coverage (relative adsorption) θi(n)l or xsi(*n)l is averaged over the entire surface (all site types) with energy distribution function χ serving as weighting factor determining relative frequencies of adsorption sites producing global/overall adsorption coverage θi(n)t or xsi(*n)t.
Global coverage:
For n-component gas mixture (n-dimensional integral):
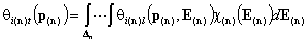
For n-solute dilute solution (solvent present in large excess is component "n+1") (n-dimensional integral):
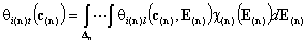
For n-component liquid mixture ((n-1)-dimensional integral):

Vectors
In the formulas bold letters denote vectors.
(n) - denotes n-element vector (gas or solute)
(*n) - is (n-1)-element vector of values relative vs. element "n" (e.g. differences for energy, ratios for equilibrium constants K and molar fractions x)
i(n) - denotes i-th component in n-component mixture (gas or solute)
i(*n) - denotes i-th component in n-component mixture (liquid mixture)
The n-element vectors:
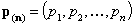 - n-element vector of pressures
- n-element vector of pressures
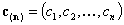 - n-element vector of concentrations
- n-element vector of concentrations
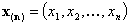 - n-element vector of molar fractions
- n-element vector of molar fractions
 - n-element vector of adsorption energies
- n-element vector of adsorption energies
The (n-1)-element vectors:
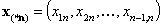 - (n-1)-element vector of molar fraction ratios
- (n-1)-element vector of molar fraction ratios
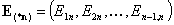 - (n-1)-element vector of adsorption energy differences
- (n-1)-element vector of adsorption energy differences
In the above:
Ei is the i-th component's reduced energy:
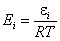 - reduced energy (more below)
- reduced energy (more below)
Eij is the reduced energy difference for components "i" and "j":
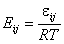 - reduced energy difference (more below)
- reduced energy difference (more below)
Competition of components "i" and "j" in liquid mixtures:
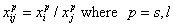 - ratio of molar fractions
- ratio of molar fractions
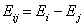 - difference of adsorption energies
- difference of adsorption energies
Energy ranges
The integration ranges:
Adsorption of single gas "i" and single solute "i":
 - energy range for component "i"
- energy range for component "i"
Adsorption in binary liquid mixture "i+j":
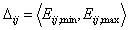 - range of energy differences for components "i" and "j"
- range of energy differences for components "i" and "j"
Multidimensional integration ranges:
Adsorption of n-component gas and n-component solute mixture (n elements):
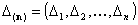 - n-element vector of energy ranges
- n-element vector of energy ranges
Adsorption in n-component liquid mixture - (n-1) elements:
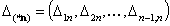 - (n-1)-element of energy differences' ranges
- (n-1)-element of energy differences' ranges
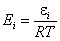 and
and 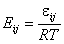 - reduced energies
- reduced energies
Local isotherm equation θl or xsl
Local isotherm equation (usually multi-Langmuir (aka Markham-Benton) isotherm for gas or dilute solute adsorption, BET for vapor adsorption and Everett for liquid mixture adsorption) corresponds to adsorption on homogeneous (i.e. energetically non-heterogeneous) surface.
For i-th component we have then the local isotherms:
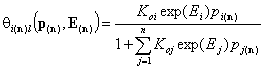 - multi-Langmuir (gas)
- multi-Langmuir (gas)
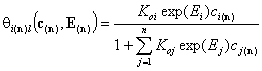 - multi-Langmuir (solute)
- multi-Langmuir (solute)
(This has sense only if reference component "n" is present):
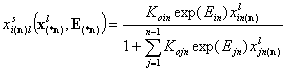 - multicomponent Everett
- multicomponent Everett
This equation may be rewritten as (as Konnexp(Enn)=1):
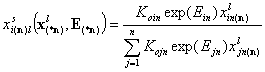 - multicomponent Everett
- multicomponent Everett
Equilibrium constants (local)
In the formulation above, the usual adsorption equilibrium constant Ki is replaced by the its relation with adsorption (reduced) energy:
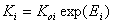 - (local) equilibrium constant for component "i"
- (local) equilibrium constant for component "i"
where Koi is the pre-exponential (or entropic) term.
Analogously, for competitive adsorption of components "i" and "j" we will have the equilibrium constant Kij related with the difference of adsorption energies (or energy change corresponding to the exchange of components "i" and "j", i.e. adsorption of "i" accompanied with desorption of "j"):
 - (local) ij-exchange equilibrium constant
- (local) ij-exchange equilibrium constant
This local isotherm equation may in general include various terms, like lateral interactions (specific and non-specific) and multilayer formation (see single gas or single solute adsorption). If lateral interactions are involved then the spatial distribution (surface topography) of adsorption sites is important.
Total local coverage by all components
An often used quantity is the coverage by all components. For gas and solute adsorption we have, respectively:
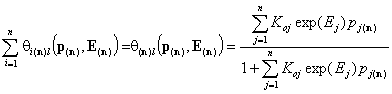 - local coverage by n-components (gas)
- local coverage by n-components (gas)
 - local coverage by n-components (solute)
- local coverage by n-components (solute)
However, for liquid mixture adsorption the sum of molar fractions of all components is always 1 (entire surface is covered all the time):
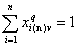 where: q = (s,l) and v=(l,t).
where: q = (s,l) and v=(l,t).
Thus we use rather the coverage by the reference component "n", xn(n) (molar fraction of component "n") or sum of molar fractions of all other (n-1) components:
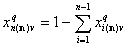 and
and
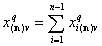
Finally we have the local surface fraction of reference component "n" (xi(*n) denotes the (n-1)-dimensional vector of ratios of molar fractions xin(n)):
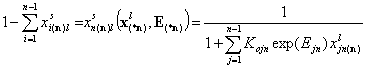 - adsorption of reference component "n"
- adsorption of reference component "n"
Total global coverage by all components
Correspondingly, we obtain expressions for global coverage by all n adsorbates (n-dimension integral):
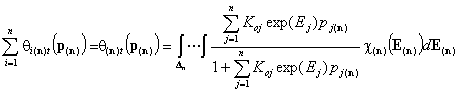 - (gas)
- (gas)
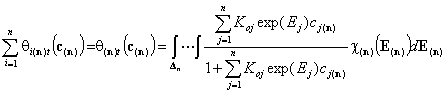 (solute)
(solute)
An for n-component liquid mixture, the global molar surface fraction of n-th component (reference component) (n-1 dimension integral):
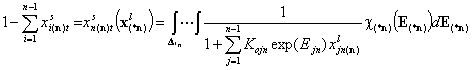
Equilibrium constants (global):
Here we may define the equilibrium constants - global/average values:
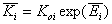 - global equilibrium constants
- global equilibrium constants
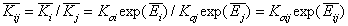 - ratio of global equilibrium constants.
- ratio of global equilibrium constants.
Those global ("average") equilibrium constants are defined for average energies or characteristic energies.
The way they are related to the characteristic (may be minimum, maximium or average or some other isotherm specific value) energy depends on the particular isotherm equation.
Those constants appear in global/overall isotherm equations, e.g. for Langmuir-Freundlich (symmetrical energy distribution, characteristic energy is average energy) we may express global isotherm of gas adsorption as: θt,LF = θt,LF(Kavp)
The material presented in this page was presented and discussed in the papers cited below and my PhD Thesis.
The presentation below differs in details from the published material, it may be treated as an extended abstract of the references below, though some of the material presented here was never published.
References:
Energy distribution function
In the above formulas, the differential form of energy distribution function was used. This form is commonly used in most descriptions of adsorption on hetereogeneous surfaces as it directly shows the frequencies (probabilties) of existing adsorption sites. However, it has some disadvantages if it comes to the description of multicomponent adsorption and especially if prediction of adsorption is to be made.
 Differential energy distribution function χ(E)
Differential energy distribution function χ(E)
Integral (cumulative) energy distribution function F(E)
The non-negative differential energy distribution function χ(E) gives relative frequencies (probabilities, P) of surface sites characterized by a some adsorption energy for a given adsorbate. This differential energy distribution χ(E) function is defined as the probability density function of adsorption energy:
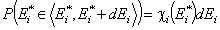
This equation may be easily reformulated in a way allowing for use of integral (cumulative) energy distribution function F(E):
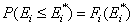
and following that we have:
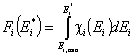 and
and
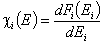
Normalization of energy distribution functions.
The integral of differential energy distribution function χ(E) over energy E is normalized to 1:
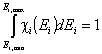 - normalization of χ(E)
- normalization of χ(E)
whereas the values of integral energy distribution functions F(E) are always between 0 and 1 (probability, always in <0,1> range):
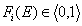 and
and
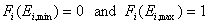
For a homogeneous surface (e.g. Langmuir isotherm):
χ(E) is defined as the Dirac's delta (impulse) function, δD(E), which is equal to 0 everywhere but in some fixed point - in this case E=Eo average and characteristic energy - and is normalized to 1; F(E) is a simple Heaviside (step) function, F(E) = 0 for E<Eo and F(E) = 1 for E≥Eo (this step function may be also defined alternately).
Mean (average) energy and shape of energy distribution function
One of the main factors in adsorption in the average adsorption energy (or position of distrbution function on energy axis):
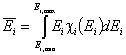 - average (reduced) energy
- average (reduced) energy
Energy function, E(F) - energy profile
In order to make integral (cumulative) energy distribytuin more useful, we have to introduce the energy function E(F) as the function inverse to the integral energy distribution function, F(E):
F(E(F)) = F
E(F(E)) = E
This energy function gives a kind of energy profile of the system - if the system is energetically homogeneous, this function is constant or - from practical point of view - almost constant. The higher the slope of E(F), the higher the system heterogeneity is.
Thus the average energy may be also calculated as:
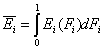 - average (reduced) energy
- average (reduced) energy
Dispersion of adsorption energy
The second factor is the width of energy distribution, which tells in a general way how much the adsorption sites are different by their adsorption energy. The most general way to compare widths of distribution functions is by comparing their energy dispersions. The definition of energy dispersion, σ, does not depend on definition of a particular distribution function (i.e. function shape, like Gauss bell-curve, continuous/Square/UNILAN, quasi-gaussian LF or Rudzinski, asymmetrical GF or Tóth etc.):
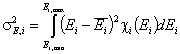 or
or
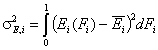
The magnitude of energy dispersion decides whether energetic heterogeneity effects will be visible in isotherm's behavior.
Henry behavior
Besides average adsorption energy and energy dispersion (or distribution width) the general shape and symmetry of energy distribution function the behavior of such function at low and high adsorption energies is very important. It affects the behavior of isotherm at very high and respectively very low pressures (concentrations) - see Henry and Langmuir behavior for low and high coverages, respectively.
General Integral Equation of Adsorption - redefined with integral (cumulative) energy distribution function F(E):
(This formulation makes it much easier to describe and analyze adsorption in multicomponent adsorption systems - see my references 1 and 2)
Simple cases:
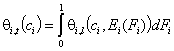 - single gas and vapor "i"
- single gas and vapor "i"
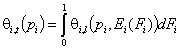 - single solute "i"
- single solute "i"
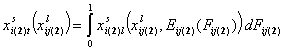 - binary liquid mixtures "i+j"
- binary liquid mixtures "i+j"
Global isotherms defined by integral (cumulative) energy distribution functions
In this formulation the adsorption energies of components do not need to be correlated (corresponding local isotherms are defined below).
Multicomponent:
n-dimensional integrals (n-component gas and solute adsorption):
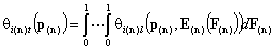 - i-th gas component
- i-th gas component
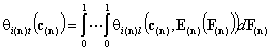 - i-th solute
- i-th solute
(n-1)-dimensional integral (n-component liquid mixture):
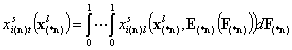 - i-th liquid component
- i-th liquid component
Local isotherms defined by integral (cumulative) energy distribution functions:
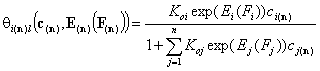 - i-th solute
- i-th solute
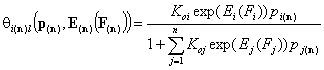 - i-th gas component
- i-th gas component
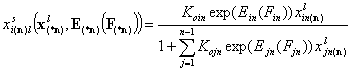 - i-th liquid component
- i-th liquid component
Vectors - non-correlated energy functions Ei(Fi) and Ein(Fin)
The n-element vectors:
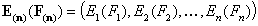 - vector of energy functions
- vector of energy functions
The (n-1)-element vectors:
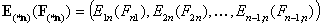 - vector of energy difference functions
- vector of energy difference functions
Special case - energy correlation
More references - energy correlation and applications
Correlation of adsorption energies
If adsorption energies of components are correlated (see model pictures), then the above n-dimensional or n-1-densional integrals may be simplified/reduced to the 1-dimensional integral. The sufficient correlation of energy means that if we order adsorption sites (types: "a","b", ... ,"z") by their adsorption energy vs. some component "i", then the order of those sites for any other component "j" will be the same.
The only allowed exception from this rule is for reference component "n" in multicomponent liquid mixtures (if we deal with differences of adsorption energies only, the order of adsorption sites obtained as above will be preserved for all component pairs "i+n", i≠n).
Correlation of adsorption energies
A simple but strong definition of energy correlation may be given as:
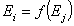 and
and
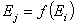 for all pairs of (i,j), i≠j
for all pairs of (i,j), i≠j
A good but less demanding definition requires, that for some component "k":
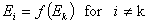
This last definition suggests also a choice of reference component "n" in liquid mixtures.
Correlation of differences of adsorption energies
For the case when we may deal directly with energy differences only (liquid mixtures), the strong version of energy correlation is:
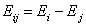 and
and
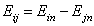 for all pairs of (i,j), i≠j
for all pairs of (i,j), i≠j
A good but less demanding definition requires, that for some component "k" and reference component "n":

Generally, the rule of thumb is that the pair (k,n) should be the component pair with the highest differences in energy distributions and the reference "n" is the component characterized by the weakest adsorption.
By using the above defined energy correlations, we may simplify the energy vectors and integral equations:
Vectors - correlated energy functions Ei(F) and Ein(F)
The n-element vectors:
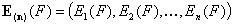 - vector of energy functions
- vector of energy functions
The (n-1)-element vectors:
 - vector of energy difference functions
- vector of energy difference functions
At the same time, for any distribution, energy correlation (or no correlation) we have ranges of F:
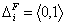 - component "i"
- component "i"
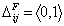 - component pair "i+j"
- component pair "i+j"
Corresponding vectors of ranges of F (non-correlated eenrgies):
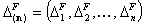 - components - n-elem.
- components - n-elem.
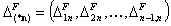 - components pairs "i+n" - (n-1)-elem.)
- components pairs "i+n" - (n-1)-elem.)
Global isotherms defined by correlated integral (cumulative) energy distribution functions
This formulation assumes the correlation of adsorption energies of components (corresponding local isotherms are defined below).
1-dimensional integrals (n-component gas and solute adsorption):
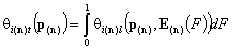 - i-th gas component
- i-th gas component
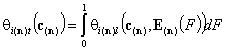 - i-th solute
- i-th solute
1-dimensional integral (n-component liquid mixture):
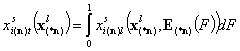 - i-th liquid component
- i-th liquid component
Local isotherms defined by correlated integral (cumulative) energy distribution functions:
Assumed correlation of adsorption energies:
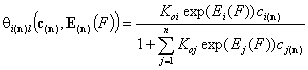 - i-th gas component
- i-th gas component
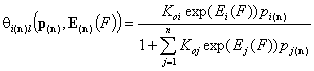 - i-th solute
- i-th solute
Assumed correlation of differences of adsorption energies:
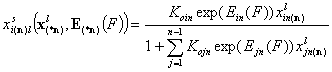 - i-th liquid component
- i-th liquid component
Global isotherms defined by correlated integral (cumulative) energy distribution functions - the local equations are insterted
This formulation assumes the correlation of adsorption energies of components (corresponding local isotherms are defined below).
1-dimensional integrals (n-component gas and solute adsorption):
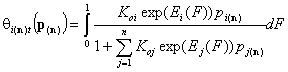 - i-th gas component
- i-th gas component
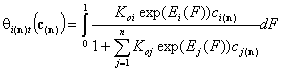 - i-th solute
- i-th solute
1-dimensional integral (n-component liquid mixture):
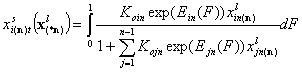 - i-th liquid component
- i-th liquid component
Separation of magnitude of adsorption energy and energy distribution shape
(see my references 1 and 2)
By rearrangement of equations and some simple definitions we may separate effects corresponding to the magnitude of adsorption energy (average adsorption energy, i.e. position of energy distribution function on the energy axis) from the general shape of energy distribution function (width or dispersion of energy distribution function). Other important parameters like minimum and maximum energy will be defined with those already defined parameters. This approach makes it easier to describe and analyse adsorption on energetically heterogeneous solids, especially in multicomponent adsorption systems.
Relative adsorption energy function, z(F)
First let us define the relative adsorption energy z=E-Eo where Eo is some characteristic adsorption energy. It may be also redefined as the inverse function to the integral (cumulative) energy distribution function, F(E), i.e. z(F)=E(F)-Eo:
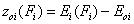 - relative energy function (relative vs. characteristic energy)
- relative energy function (relative vs. characteristic energy)
 - energy function
- energy function
This relative energy function makes it easier to analyse heterogeneity effects by extracting the relative energy changes from the adsorption energy charcateristics. The magnitude of adsorption energies is given by one simple value (characteristic energy or average energy, which may be represented by e.g. single global equlibrium constant - read further).
This characteristic energy is defined depending on the energy distribution, however it is minimum adsorption energy for GF isotherm or average adsorption energy for symmetrical energy distributions like Gauss, LF, Rudzinski etc.). The particular choice of this reference energy depends on the energy distribution (how easy is to calculate sth with some particular value), but sometimes the choice is obvious.
Often, we select characteristic energy by simple criteria:
Eo - average energy (symmetrical energy distr.)
Eo - minimum energy (energy distr. with minimum)
Eo - maximum energy (energy distr. with maximum)
For the sake of this summary I will use average energy and all variables defined with it marked with upper dash:
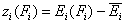 - relative energy function (relative vs. average energy)
- relative energy function (relative vs. average energy)
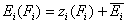 - relative energy function
- relative energy function
For the exchange of components "i" and "j" (desorption of "j" accompanied by adsorption of "i" - competitive adsorption - always in solutions) we have:
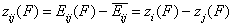 - energy difference function
- energy difference function
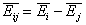 - difference of average adsorption energies
- difference of average adsorption energies
 Then we obtain energy distribution functions that define only the shape of the energy distribution, while the position (with minimum, maximum and average or characteristic energies) is defined by the characteristic or average energy:
Then we obtain energy distribution functions that define only the shape of the energy distribution, while the position (with minimum, maximum and average or characteristic energies) is defined by the characteristic or average energy: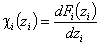 - differential relative energy distribution function
- differential relative energy distribution function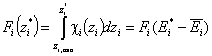 - differential relative energy distribution function
- differential relative energy distribution function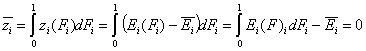
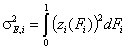
For a homogeneous surface (e.g. Langmuir isotherm):
χ(z) is defined as the Dirac's delta (impulse) function, δD(z), which is equal to 0 everywhere but in some fixed point - in this case z=0 - and is normalized to 1; F(z) is a simple Heaviside (step) function, F(z) = 0 for z<0 and F(z) = 1 for z≥0 (this step function may be also defined alternately).
General Integral Equation of Adsorption - reformulated with relative adsorption energy functions z(F):
Finally we will obtain reformulated General Integral Equation of Adsorption:
Simple cases:
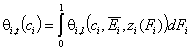 - gas and vapor phase
- gas and vapor phase
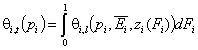 - dilute single solute
- dilute single solute
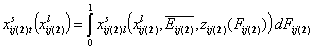 - binary liquid mixture
- binary liquid mixture
Multicomponent:
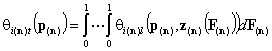 - n-dim. (gas and vapor phase)
- n-dim. (gas and vapor phase)
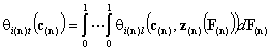 - n-dim. (dilute solutes)
- n-dim. (dilute solutes)
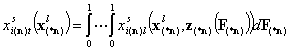 - (n-1)-dim. (liquid mixture)
- (n-1)-dim. (liquid mixture)
In these equations the average (or characteristic) adsorption energy enters the expression for adsorption equilibrium constant K of the local isotherm equation θl. Then the relative energy term z(F) corresponds only to the relative changes of the local equilibrium constant.
Special case - energy correlation
Correlation of adsorption energies and energy functions z(F)
If adsorption energies of components are correlated (just like above, see also model pictures), then the corresponding energy functions z(F) are also correlated and we may use 1-dimensional integrals in expressions for global coverage. The sufficient correlation of energy means that if we order adsorption sites (types: "s1","s2","s3" ... ) by their adsorption energy vs. some component "i", then the order of those sites for any other component "j" will be the same.
The only allowed exception from this rule is for reference component "n" in multicomponent liquid mixtures (if we deal with differences of adsorption energies only, the order of adsorption sites obtained as above will be preserved for all component pairs "i+n", i≠n).
Correlation of adsorption energies and energy functions, zi(F)
A simple but strong definition of energy correlation may be now given as:
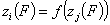 and
and
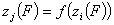 for all pairs of (i,j), i≠j
for all pairs of (i,j), i≠j
A good but less demanding definition requires, that for some component "k":
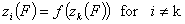
This last definition suggests also a choice of reference component "n" in liquid mixtures.
Correlation of adsorption energy difference functions, zij(F)
For the case when we may deal directly with energy differences only (liquid mixtures), the strong version of energy correlation is now:
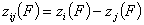 and
and
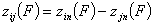 for all pairs of (i,j), i≠j
for all pairs of (i,j), i≠j
A good but less demanding definition requires, that for some component "k" and reference component "n":
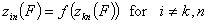
Generally, the rule of thumb is that the pair (k,n) should be the component pair with the highest differences in energy distributions and the reference "n" is the component characterized by the weakest adsorption.
For non-correlated energy functions, zi(Fi) and zin(Fin):

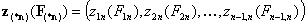
For correlated energy functions, zi(F) and zin(F):
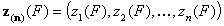
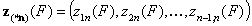
The integration ranges are now defined with respect to the relative energy changes, not energy magnitudes:
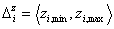 - relative energies
- relative energies
 - relative energy differences
- relative energy differences
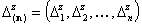 - vector of relative energy ranges
- vector of relative energy ranges
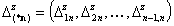 - vector of relative energy difference ranges
- vector of relative energy difference ranges
Equilibrium constants - relations
For the relative energy term zo(F) defined for the characteristic energy, Eo, we have:
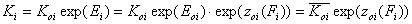 - relative vs. characteristic energy
- relative vs. characteristic energy
whereas for the relative energy term z(F) defined as relative to the average adsorption energy (default characteristic energy), we get:
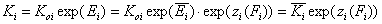 - relative vs. average energy
- relative vs. average energy
Local vs. global ("average") equilibrium constant
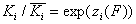 and
and
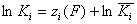
Local isotherm equations redefined with relative energy functions, z(F)
We may now rewrite local isotherm equtions by using global ("average") equilibrium constants and relative energy functions, z(F):
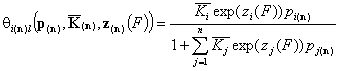
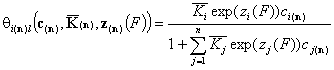
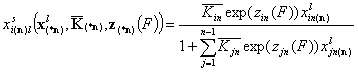
General Integral Equations redefined with relative energy functions, z(F)
 - gas
- gas
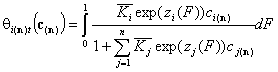 - solute
- solute
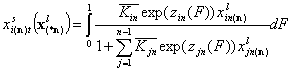 - liquid
- liquid
Adsorption in liquid phase expressed by gas/vapor adsorption energy functions
By extracting individual relative energy functions and equilibrium constants (they are impossible to measure in solution, but we may try to "guess" their values by using gas or vapor adsorption data) we rewrite the Everett equation:
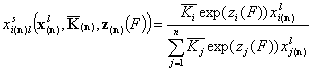
(It may be also treated as a formal multiplication of numerator and denominator by a term corresponding to adsorption of reference component "n")
Now we may obtain the General Equation of Adsorption in liquid phase expressed by gas/vapor adsorption parameters of components
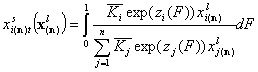
Vectors of equilibrium constants (n-element):
 - equilibrium constants
- equilibrium constants
 - average equilibrium constants
- average equilibrium constants
Vectors of equilibrium constants' ratios (n-1 elements):
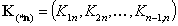 - equilibrium constants' ratios
- equilibrium constants' ratios
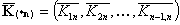 - average equilibrium constants' ratios
- average equilibrium constants' ratios
Special case - identical energy functions z(F) and F(z)
Identical integral (cumulative) distributions of relative energy F(z) of components
An often considered case of very similar components (identical heterogeneity parameters in the case of single-component adsorption data). It corresponds to identical energy distributions χi(Ei and in this formulation becomes very easy. In such a case, the corresponding relative energy functions zi(Fi) have the same shape.
If the energies are correlated, then we have:
Ei(F) = Ej(F) + ΔEij
where ΔEij is constant, and:
zi(F) = zj(F)
Local isotherms for very similar components
Then we may write the simplified local isotherms for identical relative energy functions zi(F):
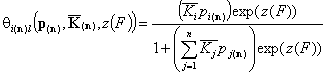
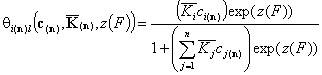
For adsorption in liquid mixture (here z(*n)(F) is the common energy "i" vs. "n" difference function):
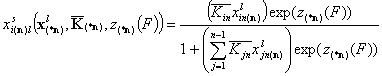
Similar components in liquid mixture
The assumption that all individual components have the same adsorption energy distribution zi(F) = z(F), leads to the conclusion, that in such a case no heterogeneity effects would be displayed because the differences of adsorption energy between components ΔEij for all pairs (i,j) would be independent of the adsorption site. Thus we may discuss the case when only (n-1) components are very similar, whereas the reference component "n" (quite often it is solvent) is different, so there are two types of heterogeneity functions present.
If the adsorption data for pure components of liquid mixture (from gas/vapor phase) are available, and we find that the distributions of n-1 components are similar, whereas the last, reference component "n" is somewhat different, then we may rewrite this last equation of local isotherm.
If z(F) is the common energy function for (n-1) components and zn(F) is the correlated energy function of the reference component "n", we have:
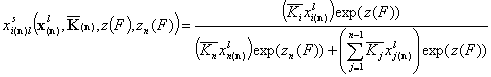 for i=1 .. n-1
for i=1 .. n-1
and for the reference component "n":
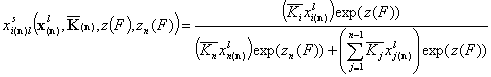
Global isotherms for very similar components
Following that we obtain simple expressions for overall adsorption of all components (sum of all components' global isotherms):
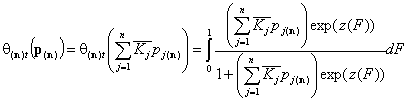 - similar gas components
- similar gas components
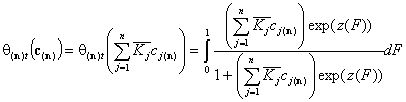 - similar solutes
- similar solutes
For n-component liquid mixture, we calculate the total adsorption of all components save n-th (reference component):


The adsorption of reference component "n" is:
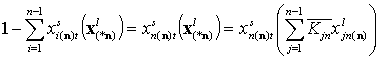
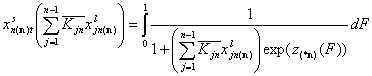
Here z(*n)(F) is the common energy "i" vs. "n" difference function. We denote it here differently to make it obvious that it is not the same as z(F) for individual components for gas and solute adsorption. Though for solute adsorption z(F) is the energy difference function too, it is perfectly clear that it is solvent-relative (solute-solvent asymmetry). However, in general liquid mixture the choice of reference component "n" seems more arbitrary ("all components are equal" - the mixtures' democracy law).
The individual adsorptions of all components may be calculated by using simple relations:
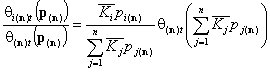
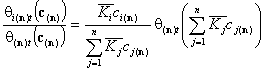

Isotherm for k reference-like mixture components
Analogously, local and global isotherm for two groups of similar components may be formulated - k of them in one group with energy function zk(F) and (n-k) components (including reference, "n") in the other, reference-like (or solvent-like) group characterized by energy function zn(F). This corresponds to the isotherm where there would be k components having the same zin(F) distribution and k components displaying no relative heterogeneity:
For relative energy difference functions:
 - for i = 1, .., k
- for i = 1, .., k
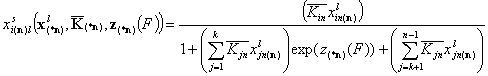 - for i = k+1, .., n
- for i = k+1, .., n
After replacing 1 with corresponding "nn" terms:
 - for i = 1, .., k
- for i = 1, .., k
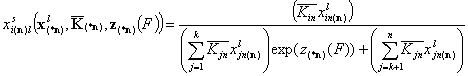 - for i = k+1, .., n
- for i = k+1, .., n
Isotherm with individual components' energy functions zn(F) and zk(F)
If we are able to separate the properties of individual components (e.g. by using single gas or vapor adsorption data or by analysis of energy correlations (see also model pictures) basing on a collection of binary systems - e.g. for 3 component systems we need binary data of "1+2", "1+3" and "2+3"), we may write this equation by using individual components' energy functions zn(F) and zk(F):
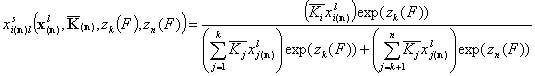 - for i = 1, .., k
- for i = 1, .., k
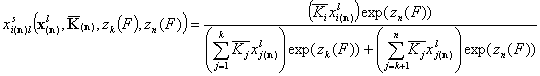 - for i = k+1, .., n
- for i = k+1, .., n
Adsorption energy - property of the entire system
One has to be always cautious while describing energy distribution function as the property of adsorbent only. Though for homogeneous adsorbents it may be true, it may change not only with the change of such adsorbate properties like functional groups, but also with changing molecular size and shape and surface topography. Moreover, in adsorption of mixtures the obtained energy distribution function may have altered - and quite different - shape and width depending on energy correlations for molecule pairs on adsorption sites (see also model pictures).
Surface site topography and lateral interactions - local isotherm:
On random topography surfaces the interaction factor depends on the mean field of adsorbate molecules which is surface-averaged anyway, i.e. it depends on the local average adsorbate density which is the same as average density of adsorbate molecules over the whole surface (that is: θl = θt) and thus does not depend on which particular site the molecule is sitting (i.e. does not depend on local adsorption energy E).
However, for patchwise topography, the density of adsorbate molecules is characteristic - and different (depending on the local adsorbate density, i.e. local coverage θl) - for each of the patches characterized with different adsorption energy E.
Global isotherm and surface topography
If for a given type of heterogeneity and without lateral interactions present the isotherm equation θt(c) (or for gas adsorption: θt(p)) has analytical form, it will be analytical with lateral interactions and random site topography, too. New isotherm θt,int(c) (or θt,int(p)) will have indentical form as the original equation if we replace concentration (or pressure for gas adsorption) by a suitable term c' = c f(θt) (or p' = p f(θt)).
For patchwise topography with lateral interactions the obtained isotherms are generally non-analytical.
Global/overall multilayer isotherm (gas or dilute solute adsorption)
May be easily obtained from its monolayer form, see for gas and vapor and solute adsorption.
Top
My papers
Search for papers
Main page
Send a message to Adam.Marczewski AT@AT umcs.lublin.pl