Quasi-gaussian distribution of errors
© A.W.Marczewski 2002
A Practical Guide to Isotherms of ADSORPTION on Heterogeneous Surfaces
Simulation of statistical deviations in experimental data:
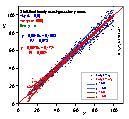
Quasi-gaussian distribution of errors




Simulation of statistical deviations in experimental data:
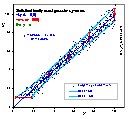
Quasi-gaussian distribution of errors with outliers

Quite often, the distribution of errors depends on variable magnitude. Then you may fit by using statistical weights or by application of data transformation that depends on the error vs. variable dependence.
Two types of deviations are shown:
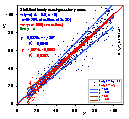
Quasi-gaussian distribution of errors was calculated by superposition of 5 random() functions (continuous distribution with total width w = 1, min = 0, max = 1, mean = 0.5) and scaling it in such a way, that the minimum and maximum were -0.5 and 0.5, respectively (total width w = 1, mean = 0):
random5() = [random()+random()+random()+random()+random()]/5 - 0.5or generally for superposition of n random() functions:
random_n() = [random()+ ... +random()]/n - 0.5Continuous random() distribution of width w has standard deviation
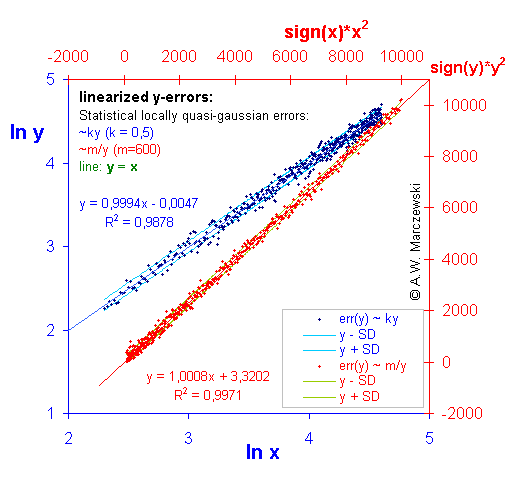
In this figure two various distributions of y-data errors are compared.
By a simple procedure required Data Transformation was obtained for each of the two cases (see next picture). The ranges of sampled data distant by σ from theoretical (initial) value are indicated by lines.
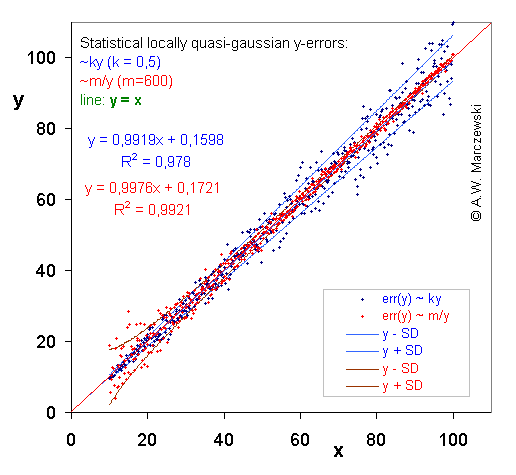
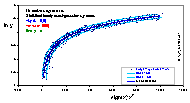
Data with y-errors simulated as described above (see previous picture) presented in appropriately transformed co-ordinates. For errors err(y) ~ ky variable y was transformed as y' = ln(y), for errors err(y) ~ m/y variable y was transformed as y' = y2. As it is easy to observe, the magnitude of errors err(y') in the transformed co-ordinates became independent of y'.
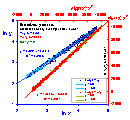
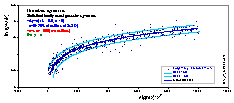
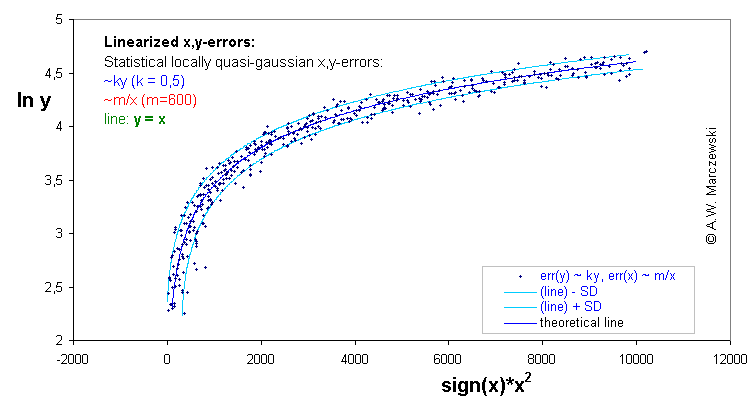
Data with simulated errors of both independent variables, err(x) ~ m/x and err(y) ~ ky. (The transformed data is shown in the next graph). The ranges of sampled data distant by σ from theoretical (initial) lines are indicated by lines.

The x,y simulated data presented in previous graph is presented in the transformed coordinates x' = x2 and y' = ln(y). The original straight line y=x isn't straight line any more - in this sense the data becomes "distorted". However, the errors have approximately uniform distribution independently of the x' and y' range.
NOTE.
Certain deviation from error independence are visible for low x',y' (and small x,y) - the transformations of data are valid if errors are small when compared with data (small relative errors) and far away from singularities of error functions (e.g. x=0 for err(x) ~ m/x) or transforming functions (y=0 for err(y) ~ ky and y'=ln(y)). However, such simple error ~ variable dependences are probably oversimplified, e.g. even if error err(y) is "proportional to y", the is always some residual error for y = 0 - background, noise etc. (you get err(y) ~ (ky+a) - see below), if err(x) ~ m/y, then most probebly it should be sth. like err(x) ~ m/(y+b), etc.
Quite often, the distribution of errors depends partially on variable magnitude. Then you may fit by using statistical weights or by application of data transformation that depends on the error vs. variable dependence.
Two types of deviations are shown:
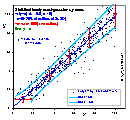
Quasi-gaussian distribution of errors was calculated by superposition of 5 random() functions (continuous distribution with total width w = 1, min = 0, max = 1, mean = 0.5) and scaling it in such a way, that the minimum and maximum were -0.5 and 0.5, respectively (total width w = 1, mean = 0) - see above. The actual random error/deviation was calculated as a product of a such simulated standarized error (w=1) by a factor dependent on magnitude of variable.
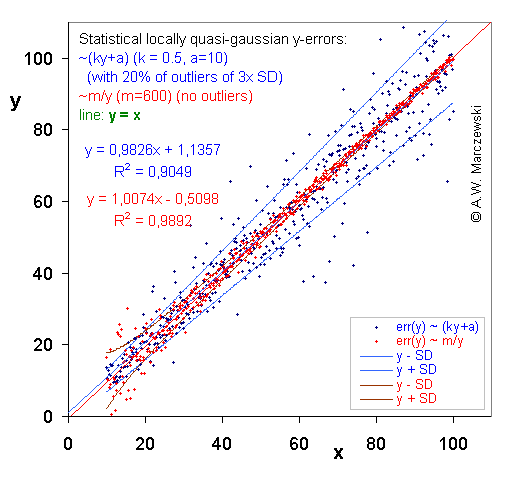
In fact two distributions were used. One - as above, i.e. without outliers - for errors err(y) ~ m/y and err(x) ~ m/x. However, the other one - distribution for errors err(y) ~ (ky+a) - was created by random switching between the original error distribution (width w1) with probability 80% and one (identical in shape/character) with probability of 20% and triple width (w2 = 3 w1), thus producing "outliers".
Quasi-gaussian distribution of errors with outliers
In this figure two various distributions of y-data errors are compared.
By a simple procedure required Data Transformation was obtained for each of the two cases (see next picture). The ranges of sampled data distant by σ from theoretical (initial) value are indicated by lines. Blue points - distribution with outliers.
Data with y-errors simulated as described above (see previous picture) presented in appropriately transformed co-ordinates. For errors err(y) ~ (ky+a) variable y was transformed as y' = ln(y+a/k), for errors err(y) ~ m/y variable y was transformed as y' = y2. As it is easy to observe, the magnitude of errors err(y') in the transformed co-ordinates became independent of y'. (Blue points - distribution with outliers).
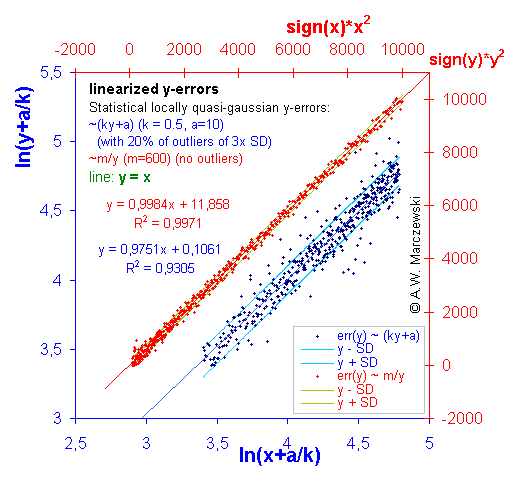
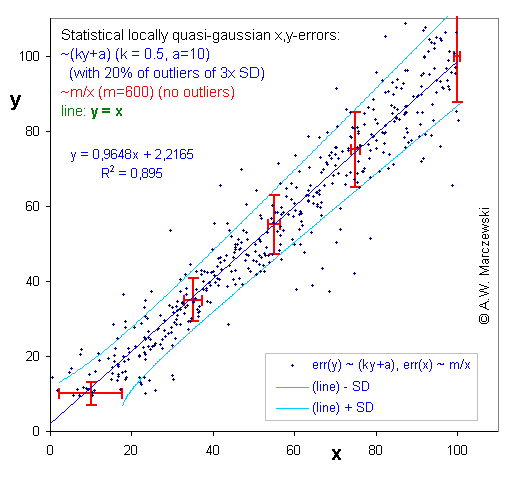
Data with simulated errors of both independent variables, err(x) ~ m/x and err(y) ~ ky+a. (The transformed data is shown in the next graph). The ranges of sampled data distant by σ from theoretical (initial) lines are indicated by lines. (Deviations of y - distribution with outliers).
The x,y simulated data presented in previous graph is presented in the transformed coordinates x' = x2 and y' = ln(y+a/k). The original straight line y=x isn't straight any more - in this sense the data becomes "distorted". However, the errors have approximately uniform distribution independently of the x' and y' range. (Deviations of y - distribution with outliers).

Send a message to Adam.Marczewski AT@AT umcs.lublin.pl