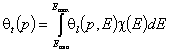 General Integral Equation of Adsorption:
General Integral Equation of Adsorption:Calculation of Energy distribution:
Stieltjes transform and
Condensation approximation (CA)
© A.W.Marczewski 2002
A Practical Guide to Isotherms of ADSORPTION on Heterogeneous Surfaces
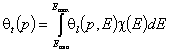 General Integral Equation of Adsorption:
General Integral Equation of Adsorption:
Calculation of Energy distribution:
Stieltjes transform and
Condensation approximation (CA)
The methods in this chapter are presented for gas adsorption only. For solute adsorption and binary liquid adsorption systems corresponding formal analogies of equations may be used.
General Integral Equation of Adsorption (GIEA) is a general formulation of adsorption isotherm involving energetical heterogeneity of the adsorption system (i.e. adsorbate-surface). The first attempt to do that was by Langmuir (1918) but it was represented by a summation not an integral.
It is quite an easy task to find/calculate the global isoterm equation if the energy distribution function was known in advance (by summation or integration). Numerical fitting of experimental isotherm is much less trivial but still manageable. However, finding a theoretical analytical equation of energy distrbution function corresponding to some - even quite simple - global theoretical isotherm may be quite difficult.
A method of solving General Integral Equation of Adsorption for local Langmuir isotherm (or any equation that may be reduced to such mathematical form) was proposed by Sips ( J.R.Sips, J.Chem.Phys., 16, 420 (1948) and 18, 1024 (1950)). It involves the so-called Stieltjes transform.
Another often used method is the so-called Condesation Approximation (CA) introduced by Roginsky (see below). This method may be used for any kind of isotherm equation, however it produces too high dispersions of energy and it fails completely for homogeneous or weakly heterogeneous surfaces. Still, it may give some insight into general shape of energy distribution function of investigated system.
Other methods include (i) approximation of energy distribution χ(E) by defined a priori analytical functions (e.g. a sum of two Gauss distributions), (ii) expansion of expressions for local isotherm θl(p,E) and energy distribution χ(E) into functional series and (iii) iterative methods (successive approximations)
Stieltjes transform
The General Integral Equation of Adsorption is the Fredholm equation of the 1st kind, where the energy distribution χ(E) is the equation kernel we are looking for:
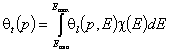
where:
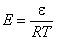 - reduced energy
- reduced energy
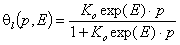 - local Langmuir isotherm
- local Langmuir isotherm
Here we make substitution of variables (pressure p and reduced energy E) by new variables y and t in order to get to the required form:
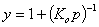

In result we have pressure p and reduced energy E defined by new variables y and t:
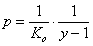
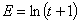
We also define a new function, G(y) = θt(1/p) by using the analytical expression for global/overall isotherm equation θt(p):
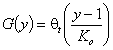
and the function f(t) which replaces the original energy distribution function χ(E):
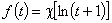
The local Langmuir isotherm is then expressed as:
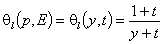
and the General Integral Equation is transformed into:
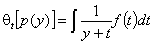
The energy distribution function χ(E) may be then obtained by back-substitution of E=E(t) in the equation (after its solving, of course!):
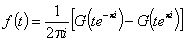
For global isotherm equation corresponding to Langmuir equation (e.g. GL equation with heterogeneity parameters m=n=1), we obtain Dirac's delta function:
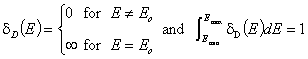
The so-called Condesation Approximation (CA) was introduced by Roginsky (S.S. Roginsky, "Adsorption and catalysis on heterogeneous surfaces", Acad.Sci.USSR, Moscow 1948 (in Russian)) and then developed by Cerofolini (G.F. Cerofolini, Thin Solid Films, 23, 129 (1074)), Jaroniec (M. Jaroniec, in: "Advances in Colloid and Interface Science", vol. 18, p.149, Elsevier, Amsterdam 1983) and others. This method may be used for any kind of isotherm equation, however it produces too high dispersions of energy and it fails completely for homogeneous or weakly heterogeneous surfaces. Still, it may give some insight into general shape of energy distribution function of investigated system.
In Condensation Approximation the local isotherm equation appropriate for a given adsorption system (e.g. Langmuir isoterm) is replaced by the stepwise function which gives coverage 0 for pressures lower than some characteristic condensation pressure, pc and coverage 1 for pressures higher than or equal to condensation pressure, pc.
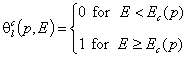 - local stepwise condensation isotherm
- local stepwise condensation isotherm
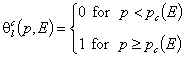 - local stepwise condensation isotherm
- local stepwise condensation isotherm
This condensation pressure pc depends on the adsorption energy, ε. In this article I will use the reduced energy E = ε/RT instead (all sources deal rather with adsorption energy, ε). If one wants to extract the adsorption energy from isotherm data, this energy is related to current isotherm pressure.
It is usually assumed that the adsorption energy E = Ec on sites being filled at p = pc corresponds to half of those sites occupied, the other half free:
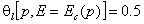
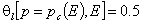
For the local Langmuir isotherm:
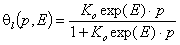 - local Langmuir isotherm
- local Langmuir isotherm
One obtains simple condition:
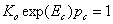
Hence the relation between condensation energy Ec corresponding to a given condensation pressure and vice versa:
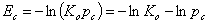
Finally simple derivative produces the energy distribution in condensation approximation:
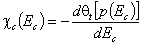
If local Langmuir isotherm with the above θl = 0.5 condition is used, then we obtain an easy-to-use formula:
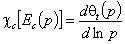
The only case where will be no CA systematic errors seems to be the infinite continuous distribution (like the one corresponding to Tiemkin isotherm), i.e. an extreme case of heterogeneity. The amount adsorbed according to the condensation approximation will be the same as the amount adsorbed according to the Langmuir model. In this case we will have also:
θt(p) = 1 - F(E)
where F(E) is the integral (cumulative) energy distribution function.
For other types of energy distribution functions the local condensation isotherm would predict: lower adsorption for adsorption energies below average energy, higher adsorption for adsorption energies above average energy. This is in agreement with the fact, that condensation approximation produces energy distrubutions corresponding to higher heterogeneities than the real ones.
Condensation Approximation (CA) - χc(E) examples
For DR (DA with n=2) and DA isotherms p ≤ po and ΔE ≥ 0 :
(p=po corresponds to ΔE=0 or E=Eo and completely filled adsorption space)
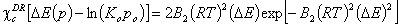 - Dubinin-Radushkevich (DR)
- Dubinin-Radushkevich (DR)
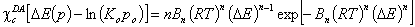 - Dubinin-Astakhov (DA)
- Dubinin-Astakhov (DA)
(Langmuir local isotherm is not consistent with the DR or DA equations - the Stieltjes transform produces energy distributions with negative regions, i.e. corresponding to negative probability of finding sites with some energy.)
For GL isotherm, ΔE = E - Eo where Eo is characteristic energy:
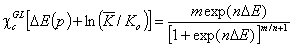 - Generalized Langmuir (GL)
- Generalized Langmuir (GL)
(Langmuir local isotherm is consistent with the GL equation, however the CA gives too wide energy distributions. Especially for homogeneous surface, where the true distribution width is 0, the CA produces energy peak with infinite tails and width at half-height ca. 4RT or 2σE=4 - i.e. 10kJ for T=298K. All GL distributions obtained by CA will also be widened.)
If you fit isotherm data to some theoretical isotherm (lets say GL isotherm or one of the other analytical isotherms you get the average or characteristic K value, i.e. value related to the adsorption energy describing position of energy distribution on the energy axis. So, by using the corresponding formulas for energy distribution it is easy to obtain energy distribution function (GL and other energy distributions). There is only one problem. The formulas say nothing about the position of distribution on the energy axis.
For each adsorption site (and adsorption energy, ε, or reduced adsorption energy, E=ε/RT) one gets the local equilibrium constant:
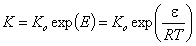
However, the value of equilibrium constant used in global/overall adsorption isotherm (e.g. in GL) corresponds to the characteristic adsorption energy, Eo which defines the position of energy distribution on the energy axis (see e.g. GL distribution). For symmetric distributions this characteristic energy is usually average adsorption energy (e.g. for LF isotherm), whereas for asymmetric ones this equilibrium constant may correspond to the minimum (e.g. for GF isotherm) or maximum energy (or some other energy - e.g. for Tóth isotherm - it depends on the adsorption isotherm used):
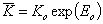 or
or
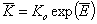
If we now define analogously to the definition used in description of energy distribution functions:
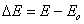 or
or
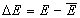
Then we may redefine the local equilibrium constants by using the "experimental" (i.e. fitted values of global/overall equilibrium constant):
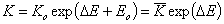 or
or
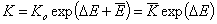
The Ko constant is often called 'pre-exponential' or 'entropic factor' and its value depends on the adsorbate, adsorbent and temperature:
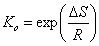
The values of this factor may be found in the literature.
E.g. for adsorption of gases (above critical temperature T3c) according to J.P.Hobson, Can.J.Phys., 43, 1934 (1965); 43, 1941 (1965) we have :
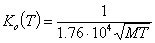 [1/Torr]
[1/Torr]
where: M is molecular mass and T is temperature.
However, below critical point, i.e. for vapor adsorption (A.W.Adamson, I.Long, L.Dormant, M.Orem, J. Colloid Interface Sci, 21, 455 (1966), L.M.Dormant, A.W.Adamson, J. Colloid Interface Sci., 38, 285 (1972)) we have:
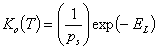
where: EL is the heat of condensation, ps is the saturation pressure.
In the formulas above the properties of adsorbent (or rather the structure of adsorption layer) are not included.
The general purpose reference may be D.M.Young, A.D.Crowell, "Physical Asorption of Gases".
You may also use my paper with example for bi-GL isotherm used for adsorption of Ar on rutile at 85K: M.Jaroniec and A.W.Marczewski, Mh.Chem., 115, 1013-1038 (1984),
(doi), "Physical Adsorption on Energetically Heterogeneous Solids.
Part II. Theoretical Extension of a Generalized Langmuir Equation and Its
Application for Analysing Adsorption Data". Adsorption data was taken from L.E.Drain,
J.A.Morrison, Trans.Faraday Soc., 48, 840 (1952)
Top
My papers
Search for papers
Main page
Send a message to Adam.Marczewski AT@AT umcs.lublin.pl