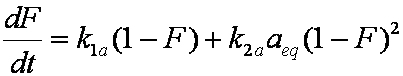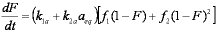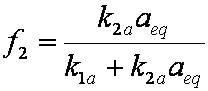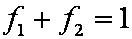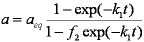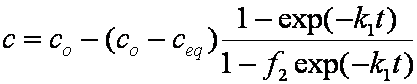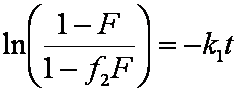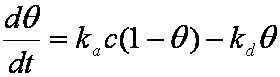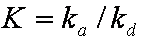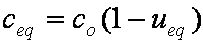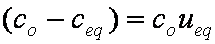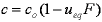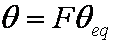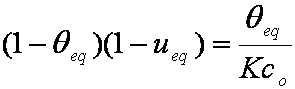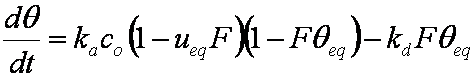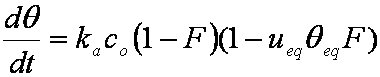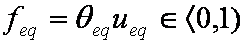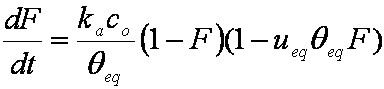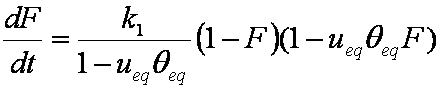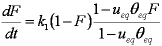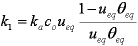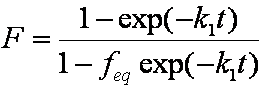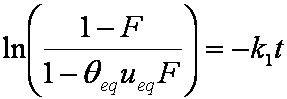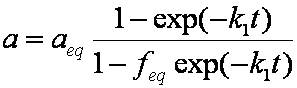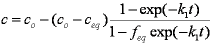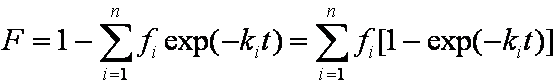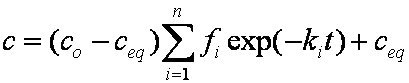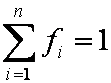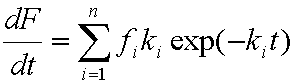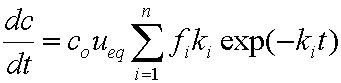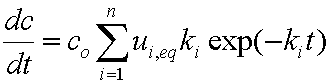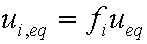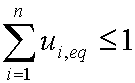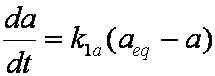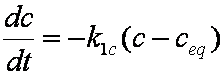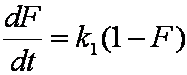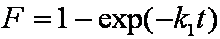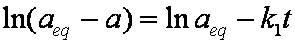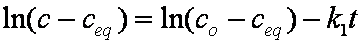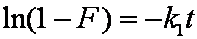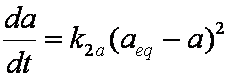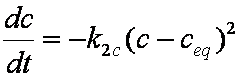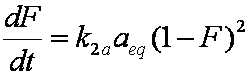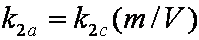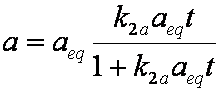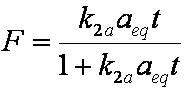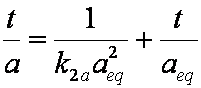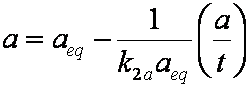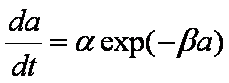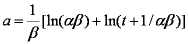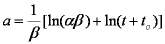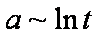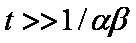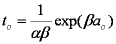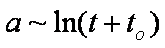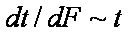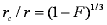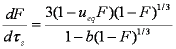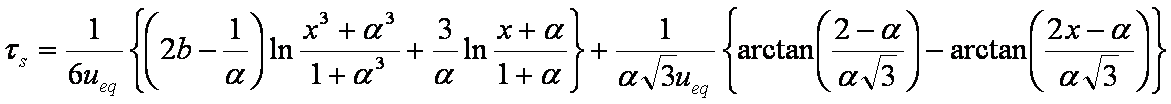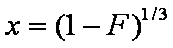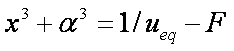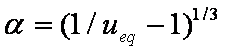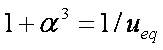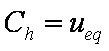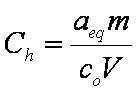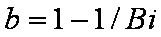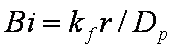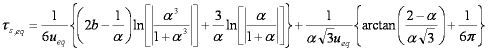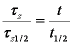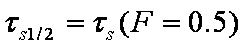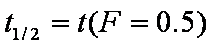Introduced and discussed by many authors, e.g. Boyd, Myers, Adamson 1947, Reichenberg 1953, Crank 1953, 1975 etc. Simplified versions are due to (Boyd, Myers and Adamson) and Reichenberg. So called Boyd eq. was developed by Boyd, Myers and Adamson. So-called Weber-Morris eq. (1963) was earlier proposed by Boyd, Myers and Adamson.
In all equations effective diffusion coefficient
Da is used:
Da = D / [τ ( 1 + ρKHεp ]
where:
D is molecular diffusion coeff., τ is (dimensionless) pore tortuosity factor,
ρ is particle density,
KH is (adsorption) Henry constant,
εp is particle porosity.
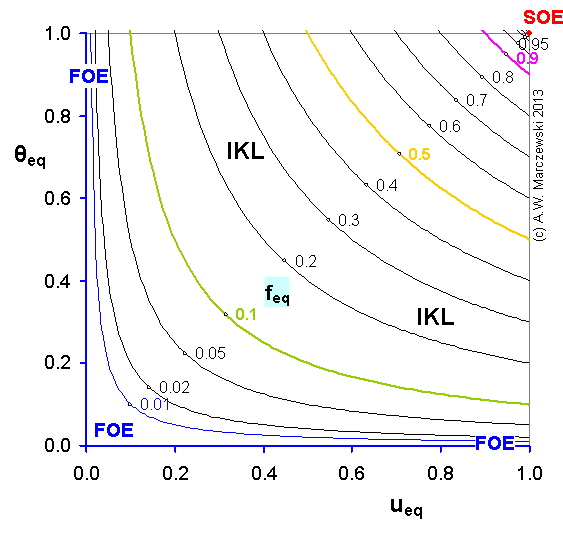
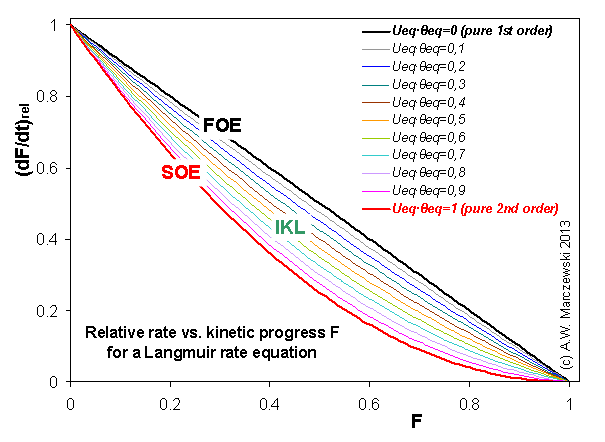
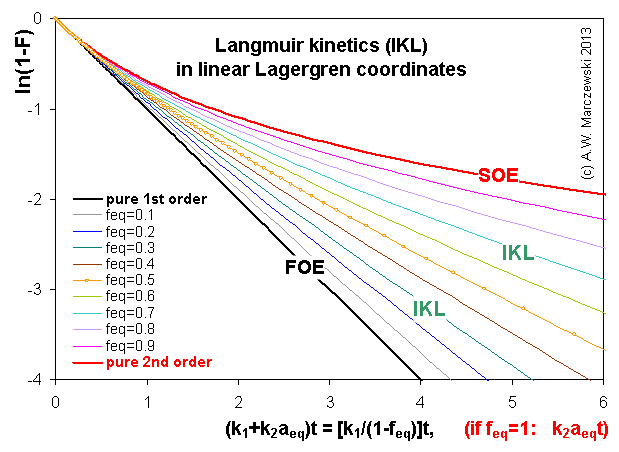
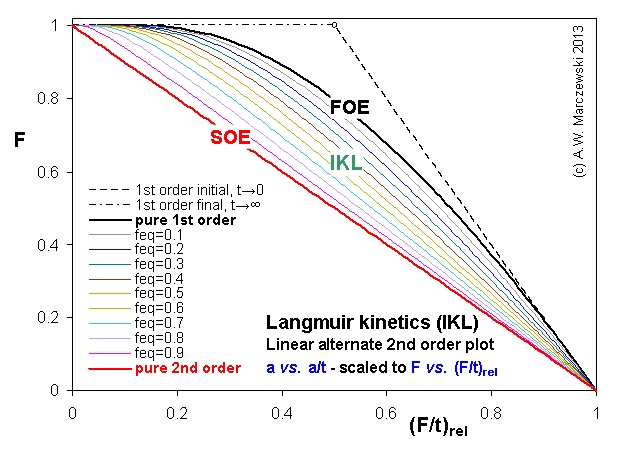
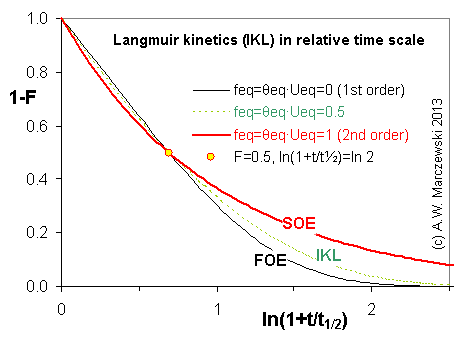
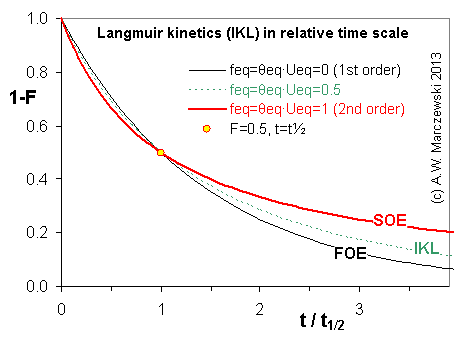
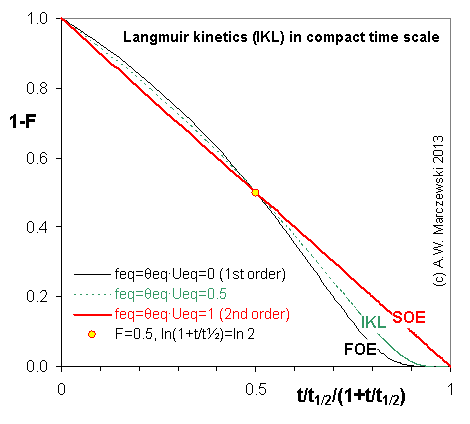
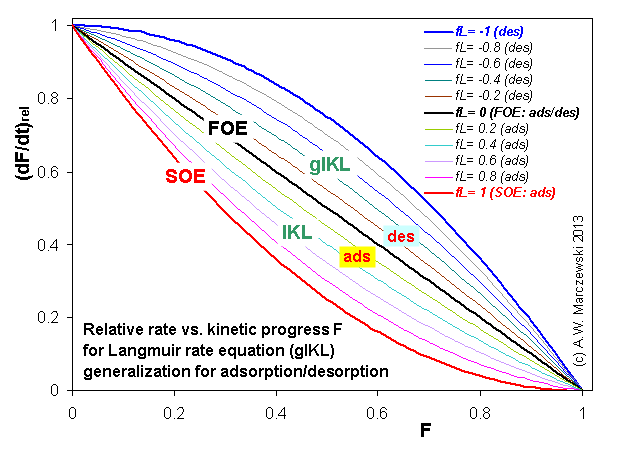
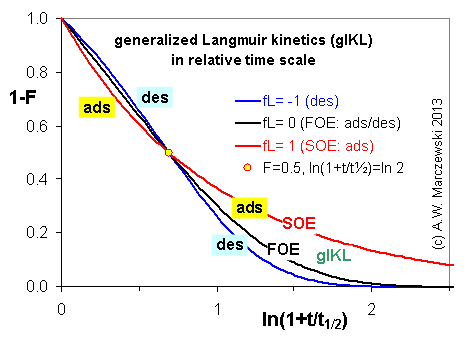
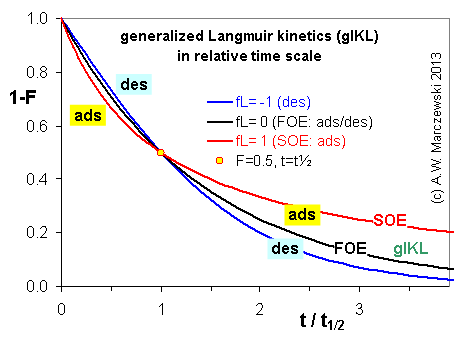
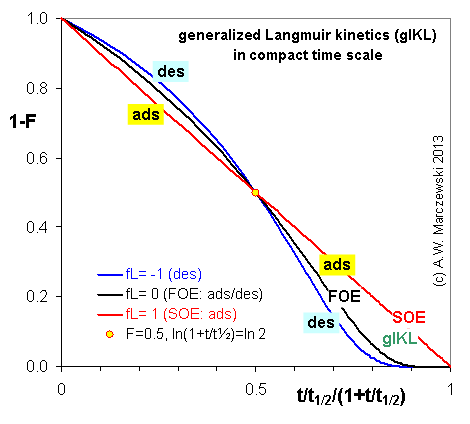
Near-equilibrium behavior is similar to the FOE/PFOE, MOE or IKL, MPFO, m-exp or any any equation with non-zero first order term in its expension series:
Boyd eq. (Boyd, Myers, Adamson 1947) - simplified, spherical particles (radius
r), near equilibrium:
F ≈ 1 - (6/π2) exp (-π2 Da t / r2)
Initial behavior:
For all various solutions (spheres or slabs, constant or varying concentration) the
infinite initial rate (da/dt)ini is obtained.
Simplified IDM (Boyd, Myers, Adamson 1947), spherical particles, low times:
F ≈ (6/r)(Dat/π)1/2
So-called
Weber-Morris eq. (1963) - simplified IDM, low times (the same as obtained by Boyd, Myers and Adamson in 1947):
a ~ t1/2
(One should note that in such a case:
da/dt ~ 1/a, see also
MPFO and
SRT)
Marczewski et al. (see Ref.
[12]) for spherical particles and varying concentration, low times:
F ≈ (1-ueq)(6/r)(Dat/π)1/2
hence,
rate dF/dt ~ 1/F:
dF/dt ≈ 0.5(1-ueq)2(6/r)2(Da/π) / F
For concentrations this solution gives:
co - c ≈ coueq (1-ueq)(6/r)(Dat/π)1/2
Good approximation (relative error < 10
-9) for low times (F < 0.5), sperical particles (radius
r) and constant concentration (uptake u
eq=0) (Reichenberg 1947):
F ≈ (6/π3/2)(Bt)1/2 - (3/π2)(Bt)
Bt ≈ 2π - π2F/3 - 2π(1 - πF/3)1/2
where
B ≈ π2Da / r2
Hence IDM half time (spherical particles, const. concentration) is approximately:
Bt0.5 ≈ 0.3015
Big problems of all these equations is the infinite initial rate. This problem may be solved by introducing some additional constraints, e.g. resistance of the external film transfer (see e.g.
PDM/McKay)
IDM equations are always given as series formulas. However, those series diverge and thus usually such formulas are suitable only for short and medium times, especially in the case of variable concentration (i.e. u
eq > 0).
Good approximations and their variants are suggested by Boyd, Myers and Adamson (1947), Carslaw and Jaeger (1947), Reichenberg (1953), Carman and Haul (1954), Crank (1956-1975), Ruthven (1984) and recently by Haynes and Lucas (2007).
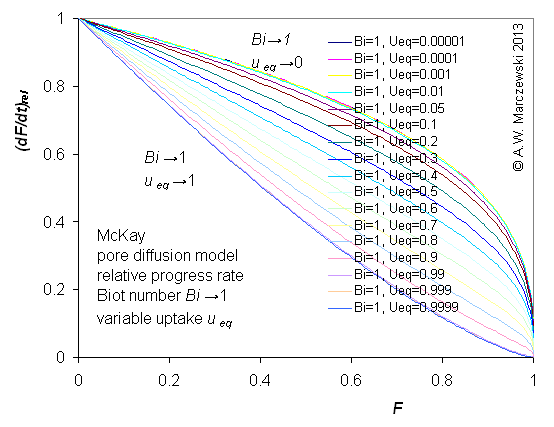
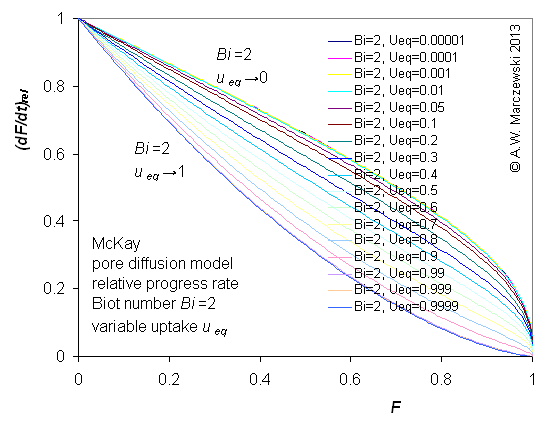
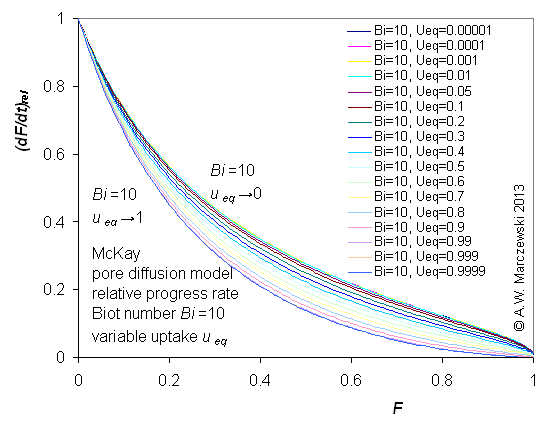
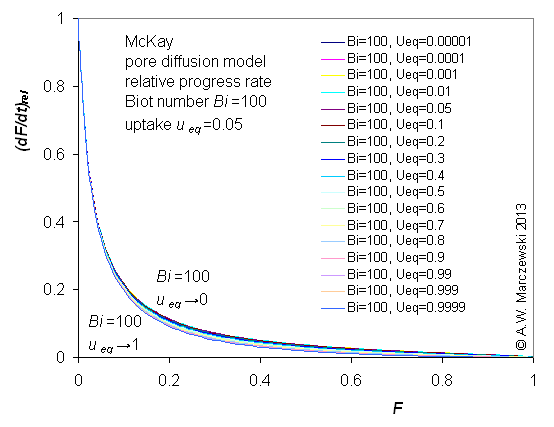
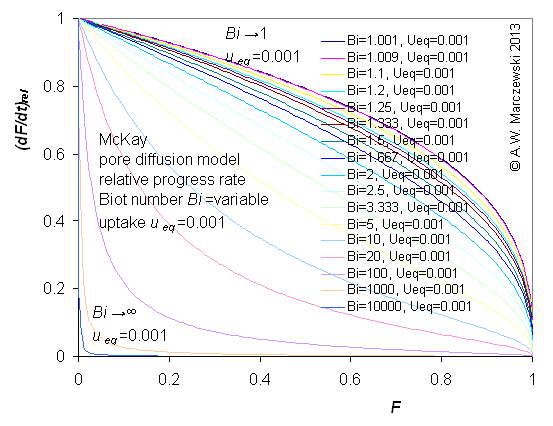
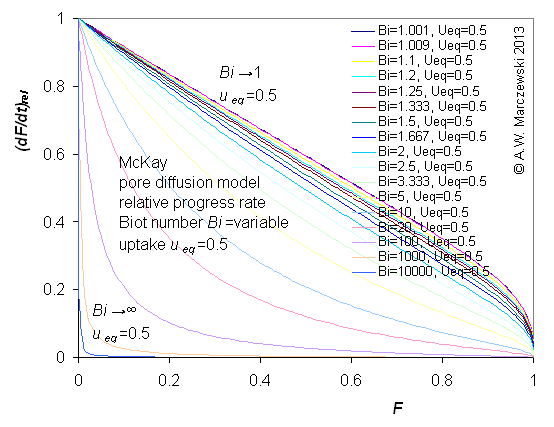
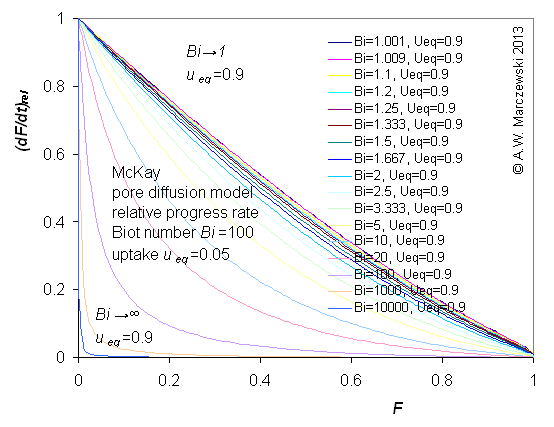
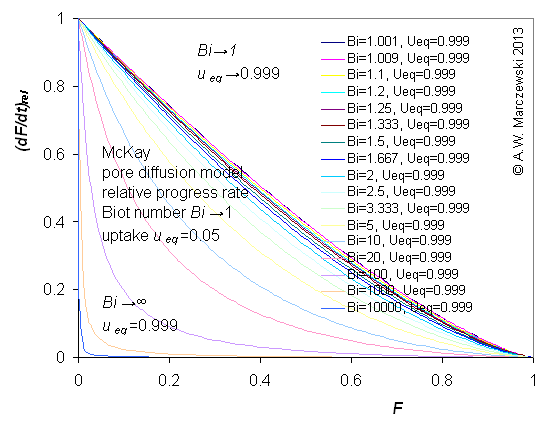
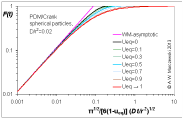
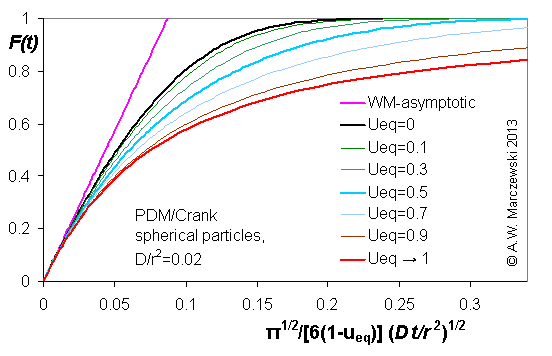
Influence of model parameters is shown in model figures (A.W. Marczewski (c) 2013).
Effect of relative uptake
ueq = 0 ... 1 (fixed D
a/t
1/2 = 0.02) shown as scaled Weber-Morris plots
F ~ t1/2 (log-log scales and linear scales):
more soon ...
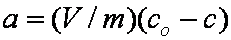 is mass balance, and
is mass balance, and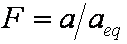 adsorption progress for adsorption on pure surface
adsorption progress for adsorption on pure surface