AWM's Adsorption page - Henry isotherm

A Practical Guide to Isotherms of ADSORPTION on Heterogeneous Surfaces

ADSORPTION:
physical consistency and Henry constant

General Integral Equation / GL (Generalized Langmuir) / All equations (preview)

Henry isotherm:

Many experimental isotherms display a behavior corresponding to the simplest isotherm, the Henry isotherm:
a = K c (for solute adsorption)
or
a = K p (for gas or vapor adsorption)

This adsorption law is formally identical with the well known Henry law for gas absorption in liquids (which in turn is a consequence of a more general Nernst partition law):
v_abs = K p (Henry law for gas absorption)

For adsorption isotherms measured in most systems this behavior may be observed for relatively high temperatures and/or very low pressures (or concentrations). However, as explained below it results from the so-called physical consistency requirement for adsorption isotherms and is a boundary condition for low relative adsorptions (coverages).

Physical consistency:
(for gas and dilute solute adsorption)

Physical consistency
Physical consistency conditions require:
- minimum and maximum adsorption energies (not fulfilled for most analytical isotherms of adsorption on heterogeneous surfaces - see below)
- isotherm with Henry region (results from max. energy condition) - if an isotherm conforms to this requirement (e.g. Tóth, Gauss) it does not mean that it fulfills the 1st one (min/max energies) - see below

Henry constant
Henry constant K_H may be defined as:
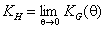where θ = a/a_m
or alternatively:
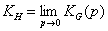or
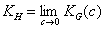
where K_G(θ) is Graham's equilibrium function:
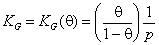for gas adsorption
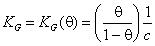for dilute solute adsorption

This condition is in fact equivalent to:
     lim_p→0(φ) = 1    or    lim_c→0(φ) = 1
where the so-called φ-function is:
     φ = δ log(a)/ δ log(p) or φ = δ log(a)/ δ log(c)

It may be shown, that for any isotherm equation θ_t(p) that does not fulfil this condition because of lack of maximum energy in its corresponding energy distribution, the Henry behavior may be obtained (forced) by a simple transformation / modification of original equation (analogously to the way the RP equation may be obtained from Henry and Freundlich isotherms):
     1/θ_t,H(p) = 1/(K_Hp) + 1/θ_t(p) (gas phase)
or
     1/θ_t,H(c) = 1/(K_Hc) + 1/θ_t(c) (solute adsorption)
The resulting isotherm will display the Henry behavior.
CAUTION! This method cannot be used to force Henry behavior for DR or DA isotherms.
If the original isotherm equation θ_t(p) ( or θ_t(c) ) displays monolayer behavior, the resulting isotherm will have such plateau, too.
The Langmuir behavior (see below) may also be forced by an analogous "trickery".
In a similar manner a Langmuir-like behaviour (see below) at p → ∞ may also be obtained. Langmuir constant K_L may be defined as:
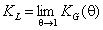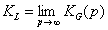or or
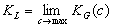
A detailed discussion and mathematical formulation for Henry and (above formulated) Langmuir constants may be found in the Appendix of the paper:
1. "Unified Theoretical Description of Physical Adsorption from Gaseous and Liquid Phases on Heterogeneous Solid Surfaces and Its Application for Predicting Multicomponent Adsorption Equilibria", A.W.Marczewski, A.Derylo-Marczewska and M.Jaroniec, Chemica Scripta, 28, 173-184 (1988) (pdf, hi-res pdf available upon e-mail request).
Physical consistency condition
It is usually believed, that the very existence of such a limit (i.e. isotherm tends to Henry behavior at very low adsorptions) is a consequence of the existing maximum of adsorption energy and is sometimes called a physical consistency condition. Though the maximum energy value always produces Henry behavior, the opposite is not necassarily true. It is easy to prove that it is enough that the energy distribution function defined in the infinite energy range (-∞ , +∞) behaves in a special way and such a limit is obtained (e.g. for Toth or RP isotherm equations).

Existence and calculation of Henry and Langmuir constants:

Calculation of Henry constant for theoretical isotherms
By using the General Integral Equation and after putting p→0 (or c→0) one easily obtains a formula being a product of 2 terms: 1^st depends only on the average adsorption energy, 2^nd is the integral that depends only on the shape and width of the energy distribution:
K_H = I₁(E_avg) I₂(σ_E)
So, e.g. for:
- "true" Gauss energy distribution, where there is no energy limit on both sides, one obtains:
  K_H = K_o exp(E_avg) exp(0.5 σ_E²)
- Langmuir-Freundlich (LF), Generalized Freundlich aka. Sips (GF) (and GL where m ≠ 1) or Rudzinski (R) equations: the 2^nd term goes to +∞ and accordingly these equations do not display Henry behaviour.
- Toth (T) or "Square" (Sq) aka. UNILAN equations: the 2^nd term is finite and accordingly these equations do display Henry behaviour.
- One may expect that the Henry constants K_H are always in the range:
  K_H ⊂ (K_avg , K_max)
  where:
  K_avg = K_o exp(E_avg) and K_max = K_o exp(E_max)
Calculation of Langmuir constant for theoretical isotherms
By using the same approach one may find an approximation of an isotherm close to monolayer filling. If such an equation reduces to Langmuir isotherm for p→∞, then an analogue of Henry constant (let's call it Langmuir equilibrium constant, K_L), may be calculated. In the calculations below it was assumed that no surface-screening effect is observed, i.e. Langmuir model and not Flory-Huggins (used e.g. for polymer adsorption) describes adsorption on homogeneous surface.
E.g. for:
- "true" Gauss energy distribution, where there is no energy limit on both sides, one obtains:
  K_L = K_o exp(E_avg) exp(-0.5 σ_E²)
- Langmuir-Freundlich (LF) or Tóth (T) (and GL where n ≠ 1) equations: the 2^nd term goes to -∞ and accordingly these equations do not display Langmuir behaviour.
- Generalized Freundlich / Sips (GF) and "Square" (Sq) aka. UNILAN equations: the 2^nd term is finite and accordingly these equations do display Langmuir behaviour.
- One may expect (provided, that lateral interactions and multilayer formation are absent) that the Langmuir constants K_L are always in the range:
  K_L ⊂ (K_min , K_avg)
  where:
  K_min = K_o exp(E_min) and K_avg = K_o exp(E_avg)
- If lateral interactions of the Fowler-Guggenheim (non-specific) or Kiselev (associative, here simplified model) must be considered (and multilayer effects are separated or non-existant), one may expect (provided, that lateral interactions are absent) that the Langmuir constants K_L are in the range:
       K_L ⊂ (K_min , K_avg)
  where:
       K_min = K_o exp(E_min) exp(α) (α - FG interaction factor)
       K_min = K_o exp(E_min) (1 + K_n) (K_n - Kiselev association constant)
  and
       K_avg = K_o exp(E_avg)
Calculability - conditions for finite values of Henry and Langmuir constants
Generally, finite values of the above 2^nd integral term are obtained if:
- for p→0 (or c→0) (Henry range):
  if for E → +∞ (or E_max) the energy distribution function decreases faster than exp(-E)
  It means that the energy distribution function with behavior described in this range by the function exp(-kE) and with 0<k<1 will not produce finite integral. However, if k>1 then the integral will be finite.
  E.g. for Tóth isotherm equation and energy distribution we have this coefficient k=(1+n)>1 (m=1, 0<n≤1 where m and n are heterogeneity coefficients)
- for p→∞ (or c→∞) ("Langmuir" range):
  if for E → -∞ (or E_min) the energy distribution function decreases faster than exp(E) (here "decrease" if you go from average energy towards -∞ or E_min)
  It means that the energy distribution function with behavior described in this range by the function exp(kE) and with 0<k<1 will not produce finite integral. However if k>1 then the integral will be finite.

General Integral Equation / GL (Generalized Langmuir) / All equations (preview)

Top
My papers
Search for papers
Main page

E-mail addresses are modified to in order to prevent spamming / mail-abuse:
in e-mail remove spaces, replace " AT@AT " by "@"

Send a message to Adam.Marczewski AT@AT umcs.lublin.pl

Disclaimer