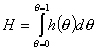 Global Heterogeneity/
Global Heterogeneity/Non-ideality concept
Concept / Formulas / Estimation / Effect separation / Isotherms / Model pictures
© A.W.Marczewski 2002
A Practical Guide to Isotherms of ADSORPTION on Heterogeneous Surfaces

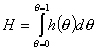 Global Heterogeneity/
Global Heterogeneity/
Non-ideality concept
Concept /
Formulas /
Estimation /
Effect separation /
Isotherms /
Model pictures
NOTE
(1) Monolayer adsorption only - if multilayer effects are visible, the isotherm must be "monolayerized", i.e. multilayer part must be estimated and removed.
(2) Localised adsorption only - infinite (+∞) integral is obtained for Volmer or Hill-deBoer adsorption isotherms (purely mobile adsorption model - perhaps one could try it for partially mobile models?). However, this approach may be reformulated in the way accomodating mobile adsorption (see below).
Global heteorgeneity, H, was introduced in 1984 (see paper below) as a possible (partial) answer to the following problems:
Why numerical (LSQ) fitting gives ambiguous answers?
(Many isotherms have similar general properties, though details of isotherm course are different and even best experimetal data is measured in a limited range of pressures/concentrations).
What is the type of non-ideality of my system?
(Heterogeneity with or without lateral interactions - only a net effect is observed because of mutual canceling).
What is the type of my adsorption isotherm?
(That is THE QUESTION!)
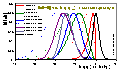
The idea came from the analysis of the two well know concepts. The concept of Graham's equilibrium function KG(θ) = θ/[(1-θ)p] proposed as a means to identify deviations form ideality. Another well known approach was the analysis of logarithmic linear plots of Langmuir and Langmuir-Freundlich equations (log[θ/(1-θ)] vs. log(p) - this kind of isotherm plot is known as the Hill plot), where for heterogeneous systems the slope coefficient m < 1, whereas for homogeneous (Langmuir) m = 1.
It was assumed that for higher heterogeneities, the characterizing value H should be higher (so slope of the linear LF-plot with swapped x-y axes was chosen as a "local heterogeneity", h(θ) function, and e.g. for LF we obtain: h(θ) = 1/m ≥ 1). Another important point was, that this specific "heterogeneity parameter" should be: independent of any specific adsorption model, relatively easy to estimate and numerically stable. As a result, integration of the log(p) vs. log[θ/(1-θ)] slope over surface coverage θ was selected as a best averaging of the isotherm local behaviour.
For larger differences between possible adsorption states H is larger. This fact explains why for example Volmer and Hill-deBoer equations give +∞ value: the effective repulsion from already adsorbed molecules grows much quicker than respective increase of pressure. It means that you must increase pressure much more than in the case of homogeneous surface (if you take the same θ starting point) to obtain the same increase of coverage. (The same as observed for heterogeneous surfaces though in this case the reason is weaker adsorption force for some of the sites which are occupied "later".)
To conclude, this concept allows to estimate a single value characterizing the entire non-ideality of the adsorption system (i.e. both adsorbate and adsorbent). By using additional adsorption data measured on homogeneous surface the lateral interaction part of the non-ideality (Hint may be separated) and a part of non-ideality related to the system energetic heterogeneity may be determined (H = HE - Hint).
As a side-effect, the system non-ideality coming from the adsorbate lateral interactions in the surface phase (but not only - see Jovanovic model below) may be estimated.
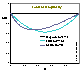
Local heterogeneity/non-ideality h(θ) function definition:
(Reciprocal of the slope coefficient of isotherm in Hill plot. High values obtained for high dispersion of adsorption energy and slow increase of adsorption with pressure at given θ - slower than for e.g. Langmuir at the same θ. This function is very sensitive to the type of non-uniformity/isotherm equation - see model pictures.)
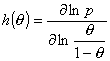
Local heterogeneity/non-ideality h(θ) function - rearranged :
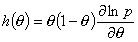
Global heterogeneity/non-ideality, H, definition:
(Local behavior h(θ) averaged over the intire isotherm - a single H value representing an entire isotherm - impossible to distinguish various types of non-uniformity.)
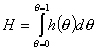
(This equation is difficult in practical application.)
Global heterogeneity/non-ideality, H, rearranged (derivatives are avoided):
(By this rearrangement avoiding the use of derivatives, the calculation of H becomes easy and insensitive to experimental errors. However the extension of calculations beyond the available experimental range <θmin - θmax> becomes a bit more difficult if no estimates of h(θmin) and h(θmax) exist - see below.)
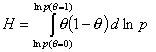
Practical calculation of Global heterogeneity/non-ideality, H, from experimental data:
The last equation should be used for estimation of global heterogeneity, H, from experimental data. However, usually a range of available coverage in adsorption measurement is much smaller then the required θ∈<0, 1>. In such a case try to do one of the following:
Separation of energetic heterogeneity (HE) and lateral interactions (Hint) effects:
Estimation from raw data of experimental adsorption on heterogeneous solid leads to:
H = HE - Hint
and alsoh(θ) = hE(θ) - hint(θ)
In order to separate both effects, a measurement of adsorption of the same adsorbate species on an energetically homogeneous surface (the same chemical/crystalochemical structure is preferred) must be performed. Then for this system Hint may easily be obtained. Finally, HE for the heterogeneous system (above) may be estimated:Hhomo = 1 - Hint
and alsohhomo(θ) = 1 - hint(θ)
Finally we get a practically useful formula:HE = Hhet(exp) + [1 - Hhomo(exp)]
For several isotherm equations h(θ) and/or H may be calculated very easily, e.g. for:
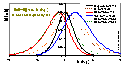 Langmuir (L) eq. (GL: m=n=1):
Langmuir (L) eq. (GL: m=n=1):
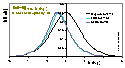 Kiselev:
Kiselev:
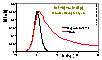 Volmer (non-localised i.e. mobile gas adsorption - mobility obstructs filling of the monolayer; analogous Hill-deBoer equation includes lateral interactions):
Volmer (non-localised i.e. mobile gas adsorption - mobility obstructs filling of the monolayer; analogous Hill-deBoer equation includes lateral interactions):
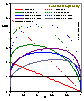
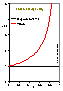
 For the equations of DA group (adsorption in micropores) analytical expressions are also obtained (for p < po or c < co):
For the equations of DA group (adsorption in micropores) analytical expressions are also obtained (for p < po or c < co):
Concept / Formulas / Estimation / Effect separation / Isotherms / Model pictures
Top
My papers
Search for papers
Main page
Send a message to Adam.Marczewski AT@AT umcs.lublin.pl