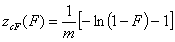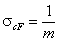© A.W.Marczewski 2002
A Practical Guide to Isotherms of ADSORPTION on Heterogeneous Surfaces
Reload Adsorption Guide
 Generalized Langmuir (GL) isotherm:
Generalized Langmuir (GL) isotherm:
[Marczewski-Jaroniec iso.]
GL energy distribution
and
Other energy distributions
see also: General Integral Equation of Adsorption and GL isotherm
see also Energy distribution and Calculation of energy distribution
see also: energy dispersion and Global Heterogeneity concept
GL Equation |
GL special forms |
GL distributions (
graphs |
functions ) | Other distr.
Alternative formulation of distributions (
GL |
Other distr. )
GL: First introduced by myself (AWM) and M. Jaroniec
"A New Isotherm Equation for Single-Solute Adsorption from Dilute Solutions on Energetically Heterogeneous Solids", A.W.Marczewski and M.Jaroniec, Mh.Chem.,
114, 711-715 (1983),
(
doi).
(theory) Mh.Chem.,
115, 997-1012 (1984),
(
doi).
(gas adsorption) Mh.Chem.,
115, 1013-1038 (1984),
(
doi).
(binary liquid adsorption) Mh.Chem.,
115, 541-550 (1984)),
(
doi).
and so on ...
NOTE
Isotherm equations below are good e.g. for dilute solutions of organics. For gas adsorption replace concentration, c, with pressure, p. If you deal with weakly soluble solutes (or your concentrations are close to solubility limit, cs) or vapours (pressures close to saturation pressure, ps), you should take it into account, e.g. by using "multilayer correction"
GL - Generalized Langmuir (aka. MJ, M-J: Marczewski-Jaroniec iso.):
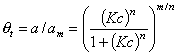
where: θt is global (overall) adsorption isotherm (overall coverage) obtained from General Integral Equation of Adsorption for Langmuir local equation and 0<m,n≤1 .
GL isotherm for specific values of parameters reduces to the simpler well known monolayer isotherm equations:
Langmuir (L) (m=n=1),
Langmuir-Freundlich (LF) (0 < m=n ≤ 1),
Generalized Freundlich (GF) aka. Sips eq. (n=1, 0 < m ≤ 1) and
Toth (T) (m=1, 0 < n ≤ 1)).
Generally parameter m is responsible for the isotherm behaviour at c → 0 (and ΔE → +∞) whereas n for the course at c → ∞ (and ΔE → -∞). This equation may be extended to lateral interactions and multilayer.
Model energy distribution functions for GL and its special cases (generally parameter m is responsible for the behaviour at ΔE → +∞ and n for ΔE → -∞):
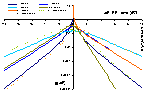
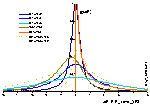
Energy distribution functions and their asymptotes (generally parameter m is responsible for the behaviour at ΔE → +∞ and n for ΔE → -∞):
-
Langmuir, L (m=n=1) isotherm (homogeneous)
Energy distribution function χ(E) is defined by Dirac's delta (impulse) function, δD(E)
-
Generalized Langmuir, GL (m≠n, m≠1, n≠1) isotherm
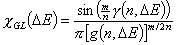
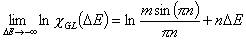
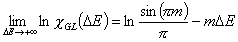
-
Langmuir-Freundlich, LF (m=n, n≠1) isotherm
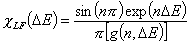
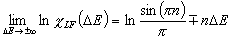
-
Tóth (m=1, n≠1) isotherm
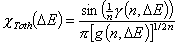
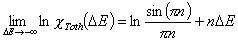
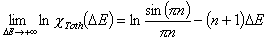
-
Generalized Freundlich, GF (n=1, m≠1) isotherm (ΔE > 0 - see below)
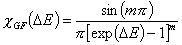
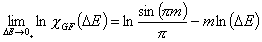
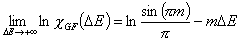
In the above equations:
- ΔE = E - Eo
- E = ε/RT is reduced energy
- Eo is a characteristic energy.
for symmetrical LF: Eo = Eavg (average energy)
for asymmetrical GF: Eo = Emin (minimum energy)
-
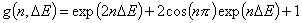
-
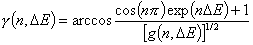 or
or
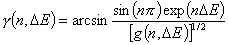
Other energy distribution functions and their asymptotes:
Alternative formulations of energy distribution functions
See General Integral Equation of Adsorption
Based on:
- "Unified Theoretical Description of Physical Adsorption from Gaseous and Liquid Phases on Heterogeneous Solid Surfaces and Its Application for Predicting Multicomponent Adsorption Equilibria", A.W.Marczewski, A.Derylo-Marczewska and M.Jaroniec, Chemica Scripta, 28, 173-184 (1988) (pdf, hi-res pdf available upon e-mail request).
- "A Simplified Integral Equation for Adsorption of Gas Mixtures on Heterogeneous Surfaces", A.W.Marczewski, A.Derylo-Marczewska and M.Jaroniec, Mh.Chem., 120, 225-230 (1989),
(doi).
- "Prediction of the Heterogeneity Parameters for Adsorption of Multicomponent Liquid Mixtures on Solids", A.W.Marczewski, A.Derylo-Marczewska, M.Jaroniec and J.Oscik, Z.phys.Chem., 270(4), 834-838 (1989)
(pdf, hi-res pdf available upon e-mail request).
The same distributions may be expressed through the z = E-Eo (ΔE in the formulas above), where Eo is characteristic energy, and the integral (cumulative) energy distribution function F(E) or F(z) (see references above and General Integral Equation of Adsorption).
In the following formulas:
-
ΔE = Emax - Emin (for finite-width distributions)
-
z = E - Eo - where Eo is characteristic energy (see above);
Unless specified otherwise:
Eo is average energy for symmetric distributions;
Eo is Emin or Emax for asymmetric energy distributions with minimum and maximum energy, respectively.
-
F(E), F(z) - integral (cumulative) energy distribution function, 0≤F≤1
-
χ(z) = dF(z)/dz, χ(E) = dF(E)/dE - differential energy distribution function
(For a homogeneous surface - e.g. Langmuir eq. - χ(z) is defined as the Dirac's delta, δD(z), which is equal to 0 everywhere but in some fixed point - in this case z=0 - and is normalized to 1; F(z) is a simple Heaviside (step) function, F(z) = 0 for z<0 and F(z) = 1 for z≥0 - may be also defined alternately)
Energy distributions and energy dispersions:
CAUTION!
Over a period of 3 days (Nov.5 - Nov.7, 2003) there were some erroneous formulas for energy dispersion for LF, GF and Tóth (opposite sign of expression under square root) and z(F) for Sq (1-F instead of F-0.5). There were also some minor inconsistencies in parameter naming schemes (m or n).
-
Langmuir, L (m=n=1) isotherm (homogeneous)
Differential energy distribution function χ(z) is defined by Dirac's delta (impulse) function, δD(z) and the integral (cumulative) energy distribution function is defined by the simple Heaviside (step) function (Heaviside function defined alternately)
-
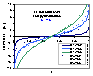
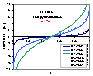 Langmuir-Freundlich, LF (m=n), -∞<z<+∞
Langmuir-Freundlich, LF (m=n), -∞<z<+∞
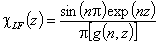 where
where
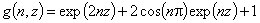
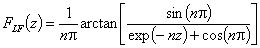 (direct formula for z≤0 and F≤0.5)
(direct formula for z≤0 and F≤0.5)
For z>0 and F>0.5 use symmetry: F(z) = 1-F(-z)
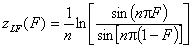
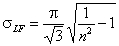
-
Generalized-Freundlich, GF (n=1), z>0
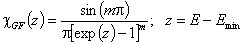
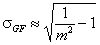
-
Tóth isotherm (m=1), -∞<z<+∞
Eo is characteristic energy (it is not average energy here)
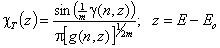 where
where
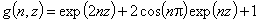 and
and
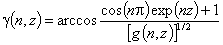
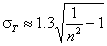
And also:
-
Gauss distribution (σ > 0), -∞<z<+∞
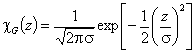 and
and
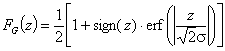
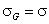
-

 Rudzinski, R (0 < m < ∞), -∞<z<+∞
Rudzinski, R (0 < m < ∞), -∞<z<+∞
This equation will behave similarly to LF if:
-
mR = nLF (at θ→0 and θ→1 - very low and very high energies)
-
σR = σLF (at moderate coverages and energies)
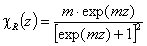
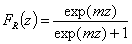 and
and
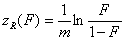
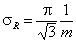
-
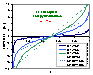 Square (continuous, fixed width ΔE > 0) aka UNILAN
Square (continuous, fixed width ΔE > 0) aka UNILAN
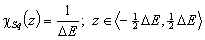
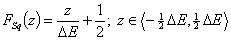 and
and
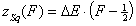
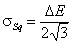
-
 k-centered discrete (fixed width ΔE > 0, k ≥ 2)
k-centered discrete (fixed width ΔE > 0, k ≥ 2)
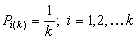 and
and
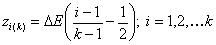
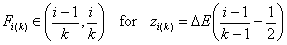 and
and
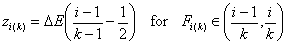
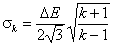
-
cut Freundlich, cF (decreasing exponential with minimum energy Emin, m > 0)
Here: characteristic energy, Eo = Emin + 1/m = Eav (average energy)

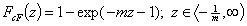 and
and
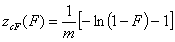
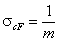
GL Equation |
GL special forms |
GL distributions (
graphs |
functions ) | Other distr.
Alternative formulation of distributions (
GL |
Other distr. )
Top
My papers
Search for papers
Main page
E-mail addresses are modified to in order to prevent spamming / mail-abuse:
in e-mail remove spaces, replace " AT@AT " by "@"
Send a message to Adam.Marczewski AT@AT umcs.lublin.pl
Disclaimer
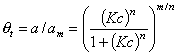 Generalized Langmuir (GL) isotherm:
Generalized Langmuir (GL) isotherm:
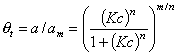 Generalized Langmuir (GL) isotherm:
Generalized Langmuir (GL) isotherm:
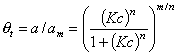


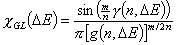
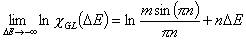
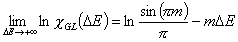
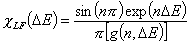
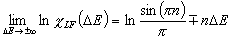
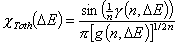
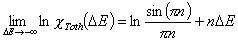
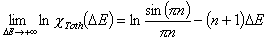
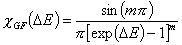
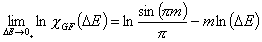
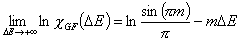
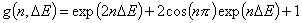
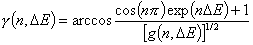 or
or
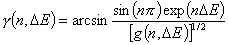
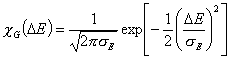
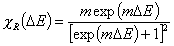
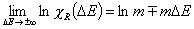

 Langmuir-Freundlich, LF (m=n), -∞<z<+∞
Langmuir-Freundlich, LF (m=n), -∞<z<+∞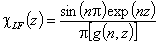 where
where
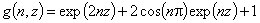
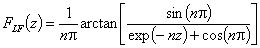 (direct formula for z≤0 and F≤0.5)
(direct formula for z≤0 and F≤0.5)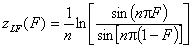
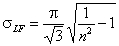
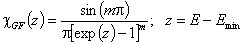
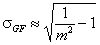
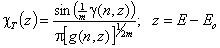 where
where 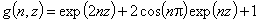 and
and
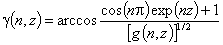
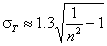
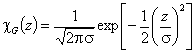 and
and
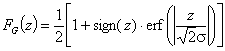
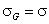

 Rudzinski, R (0 < m < ∞), -∞<z<+∞
Rudzinski, R (0 < m < ∞), -∞<z<+∞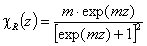
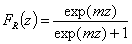 and
and
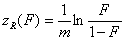
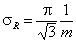
 Square (continuous, fixed width ΔE > 0) aka UNILAN
Square (continuous, fixed width ΔE > 0) aka UNILAN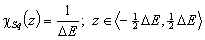
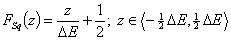 and
and
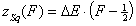
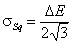
 k-centered discrete (fixed width ΔE > 0, k ≥ 2)
k-centered discrete (fixed width ΔE > 0, k ≥ 2)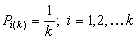 and
and
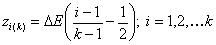
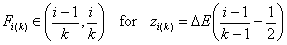 and
and
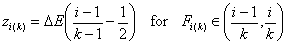
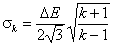

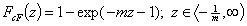 and
and