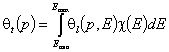 General Integral Equation of Adsorption:
General Integral Equation of Adsorption:Single gas adsorption
© A.W.Marczewski 2002
A Practical Guide to Isotherms of ADSORPTION on Heterogeneous Surfaces
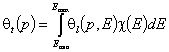 General Integral Equation of Adsorption:
General Integral Equation of Adsorption:
Single gas adsorption
see G.I.E.A. for dilute single-solute and binary liquid adsorption
see G.I.E.A. for multicomponent adsorption
isotherm equations |
GL isotherm
GL energy distribution |
energy dispersion |
Global Heterogeneity
NOTE
Equations below are good e.g. for gas and vapor adsorption. If you deal with vapors with pressures close to saturation pressure, ps you should take it into account, e.g. by using "multilayer correction" - see below.
General Integral Equation of Adsorption (GIE) is a general formulation of adsorption isotherm involving energetical heterogeneity of the adsorption system (i.e. adsorbate-surface).
The first attempt to describe adsorption on non-homogeneous solids was by Langmuir (1918) but it was represented by a simple summation not an integral.
Another similar in character Integral Equation of Adsorption is the Stoeckli integral equation for adsorption on microporous non-uniform solids.
General Integral Equation of Adsorption
For single gas adsorption
(see GIE for dilute single-solute and binary liquid adsorption or multicomponent adsorption)
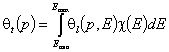 - for gas adsorption
- for gas adsorption
where: θt is global (overall) adsorption isotherm (overall coverage) and θl is local adsorption isotherm (local coverage), χ(E) is energy distribution function (see χ(E) functions and χ(E) model pictures for GL isotherm) and E is reduced adsorption energy (E=ε/RT where ε - energy). For many theoretical isotherms energy range extends from -∞ to +∞. It is not physically consistent, but with some notable exceptions (e.g. Sq isotherm), global isotherms obtained for limited energy range have no simple analytical representations.
Energy distribution function
see also a section in General Integral Equation
CAUTION!
One has to be always cautious while describing energy distribution function as the property of adsorbent only. Though for homogeneous adsorbents it may be true, it may change not only with the change of such adsorbate properties like functional groups, but also with changing molecular size, shape and surface topography. Moreover, in adsorption of mixtures the obtained energy distribution function may have altered - and quite different - shape and width depending on energy correlations for molecule pairs on adsorption sites.
Monolayer
Local Langmuir isotherm:
Localised monolayer physical adsorption (another local isotherm may be e.g. Jovanovic eq.):
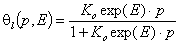
where: Ko is entropy-related and temperature dependent constant (so-called pre-exponential factor), sites are characterised by reduced energy E (or rather reduced energy of adsorption of a given molecule on certain site is E).
Local Langmuir isotherm with lateral interactions included:
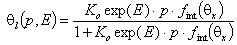
where: fint(θx) denotes interaction factor and θx is relative surface coverage (local or overall depending on surface topography):
for random site topography: θx=θt (global coverage)
for pathwise topography: θx=θl (local coverage).
Surface site topography and lateral interactions:
The reason for such a difference is that on random topography surfaces the interaction factor depends on the mean field of adsorbate molecules which is surface-averaged anyway, i.e. it depends on the local average adsorbate density which is the same as average density of adsorbate molecules over the whole surface (that is: θl,avg = θt) and thus does not depend on which particular site the molecule is sitting (i.e. does not depend on local adsorption energy E).
However, for patchwise topography, the density of adsorbate molecules is characteristic - and different (depending on the local adsorbate density, i.e. local coverage θl) - for each of the patches characterized with different adsorption energy E.
For (simplified) Kiselev (association, i.e. specific lateral interactions in surface phase) and Fowler-Guggenheim (Van der Waals, i.e. non-specific lateral interactions in mean field approximation) we get interaction factors, respectively:
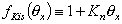 (Kiselev)
(Kiselev)
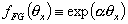 (Fowler-Guggenheim)
(Fowler-Guggenheim)
The above Kiselev interaction form is a simplified equation, the form of full Kiselev equation is more complicated and may involve also lateral non-specific (FG mean-field) interactions:
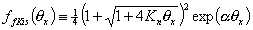
This factor may be simplified in some cases:
for Knθx >> 1 :
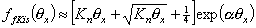
for Knθx << 1 :
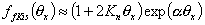
One may also see, that the association constant Kn in simplified Kiselev equation has an approximate value of 2Kn of the full Kiselev equation (if of course we assume that non-specific interaction term α=0).
NOTE on random/patchwise topographies.
If for a given type of heterogeneity and without lateral interactions present the isotherm equation θt(p) has analytical form, it will be analytical with lateral interactions and random site topography, too. New isotherm θt,int(p) will have indentical form as the original equation if we replace concentration (or pressure for gas adsorption) by a suitable term p' = p f(θt).
For patchwise topography with lateral interactions the obtained isotherms are generally non-analytical.
Multilayer
Local Langmuir + multilayer isotherm, where x=p/ps :
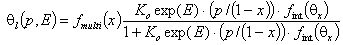
For BET model (See other multilayer isotherms) a multilayer factor fmulti(x) is:
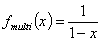
Global/overall multilayer isotherm is easily obtained from its monolayer form θt(p) by replacing p with p/(1-x) and including fmulti(x):
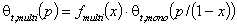
Top
My papers
Search for papers
Main page
Send a message to Adam.Marczewski AT@AT umcs.lublin.pl